Brückenbogen?Ganzrationale Funktion?
Hallo Leute ,
ich verstehe die Aufgabe nicht ganz.War die letzten Tage krank und muss alles nachholen.Selbst meine Klassenkameraden sind verzweifelt.
Die Aufgabe lautet:
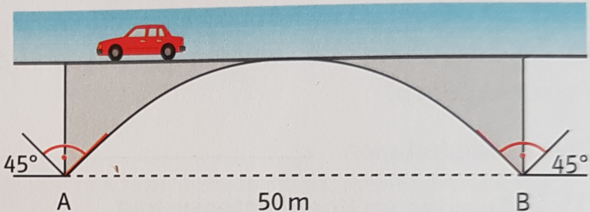
Ein Brückenbogen überspannt einen 50m breiten Geländeeinschnitt.In A und B setzt der Bogen senkrecht an den Böschungen auf(Vgl.Figur 2)
Wählen Sie ein geeignetes Koordinatensystem,bestimmen Sie eine ganzrationale Funktion 2.Grades und berechnen Sie die Höhe des Brückenbogens.
Ansatz:Das Koordinatensystem habe ich so angelegt,dass die 50m jeweils geteilt werden,so dass ich 25 habe.Diese wären theoretisch die Nullstellen.
Funktion 2.Grades :f(x)=ax^2+bx+c
f´(x)=2ax+b
Habe die falschen Bedingungen aufgestellt.Weiß nicht wieso die Steigung 1 beträgt.
Gruß SelenaFan2002
6 Antworten
Addieren der beiden Gleichungen ergibt 2b = 0, also b = 0.
Einsetzen von b = 0 in die Gleichung 50a + b = -1 ergibt
50a = -1, also a = -1/50
Einsetzen von a = -1/50 und b = 0 in die Gleichung 625a + 25b + c = 0 ergibt
-25/2 + c = 0, also c = 25/2.
Tipp: Wenn du schon leicht an die Nullstellen herankommst, verwende doch die Nullstellenform
f(x)=a(x-x1)(x-x2)
als Ansatz für deine Funktion.
Warum fragst du mich das? ;) Wenn du die Nullstellenform nutzt, hast du nur eine Gleichung für den Parameter a, denn die beiden Nullstellen kannst du direkt einsetzen!
Aber um deine Frage trotzdem zu beantworten, die dritte Bedingung könnte sein f(-25)=0.
Übrigens ist die zweite Bedingung nicht ganz richtig, es sollte sein
f'(-25)=1 oder f'(25)=-1.
Achso in der Schule haben wir das bisher anders gemacht.Deswegen:-)
Mene Freundin hat eine andere Schreibweise
Nun, wenn man viele Nullstellen kennt (in dem Fall kennst du sogar alle beide), dann ist es immer eine gute Idee die Nullstellenform zu nutzen. Du kannst ja deinen Lehrer mal fragen, wie er das sieht!
Hallo,
die Steigung einer Funktion ist der Tangens des Winkels, den eine Tangente an den Funktionsgraphen mit der x-Achse bildet.
Da der Winkel hier 45° beträgt und tan (45)=1, ist die Steigung am linken Rand gleich 1.
Am rechten Rand beträgt sie dann -1, denn hier fällt der Graph in gleicher Weise, wie er auf der anderen Seite steigt (Symmetrie).
Du hast also f(25)=0 und f'(-25)=1.
Da die Funktion achsensymmetrisch ist (lege die y-Achse durch den Scheitelpunkt), fällt das x-Glied weg. f(x)=ax²+b.
f'(x)=2ax
Zwei Unbekannte, nämlich a und b, zwei Gleichungen.
Das sollte zu schaffen sein.
Herzliche Grüße,
Willy
Bei mir kommt a=0.02 raus.Das ist positiv,aber dann ist das doch keine nach unten geöfnete Parabel.
Dann hast Du beim Umstellen der Gleichung einen Vorzeichenfehler gemacht.
Ich habe a=-0,02 und b=12,5, was dann auch die Höhe der Brücke ist.
Hast Du daran gedacht, daß f'(25)=-1 ist und nicht 1?
f(25)=0 bedeutet: a*25²+b=0
b=-625a
f'(25)=-1 bedeutet 50a=-1, also a=-1/50=-0,02.
Die Steigung an A und B beträgt doch 1, weil jeweils einen 45°-Winkel hast.
Die Steigung beträgt 1, weil die Brückenpfeiler mit einer Steigung von 45° anfängt. Steht ja da. tan(45)=1
Achso.Da kommt eine Dezimalzahl raus:Hat mich deswegen irritiert.
Wie mache ich das eigentlich mit der Schreibweise des linearen Gleichungssystems.Dazu benötige ich Bedingungen.Funktion 2,Grades,also 3 Bedingungen....
f(25)=625a+25b+c=0
f´(25)=50a+b=1
Wie kriege ich c weg?
:-)
Das sind 2 Bedingungen die 3.weiß ich nicht.