Brauche Hilfe bei neuen Mathe Thema stochastik unabhängig oder nicht?
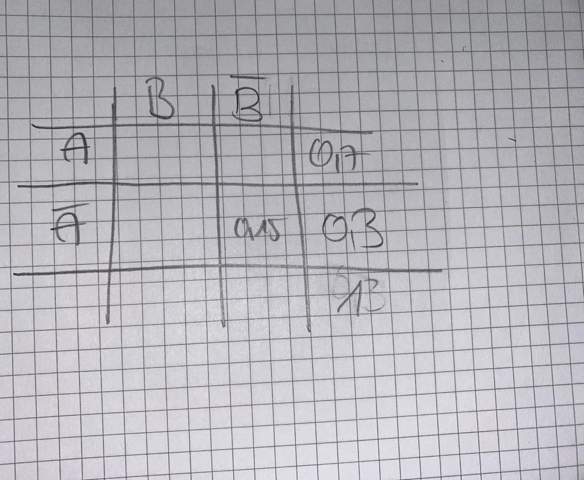
Das Thema konnte ich schon nie und jz noch das ich komm bei Aufgabe 2 und 3 einfach nicht weiter hab’s mit einer Vierfeldertafel bei A2 versucht. Trotzdem alles falsch

2 Antworten
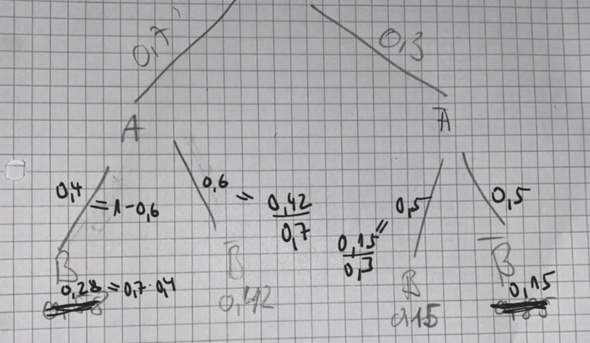
Die Wahrscheinlichkeit für den linken Zweig steht am Zweig selbst.
Die Zahlen 0,42 und 0,15 stehen unter den Endknoten des Baumes, deshalb würde ich vermuten, dass es sich um die endgültigen Wahrscheinlichkeiten handelt.
Demnach müssten die Wahrscheinlichkeiten
für A->B (0,7 - 0,42) sein und
für (nicht-A)->(nicht-B) (0,3-0,15) sein
Daraus kannst du die Wahrscheinlichkeiten der Zweige der 2. Stufe ausrechnen.
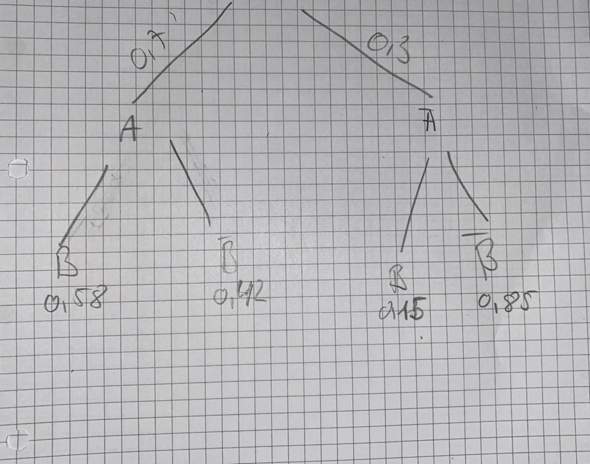
Wenn hier die beiden linken Zweige dieselbe Wahrscheinlichkeit haben und ebenso die beiden rechten, sind A und B stochatisch unabhängig, sonst sind sie stochastisch abhängig.
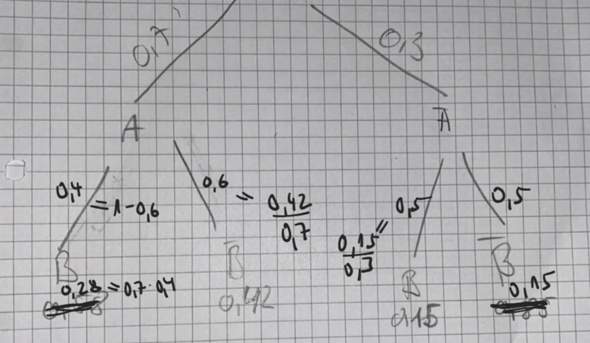
Die Ereignisse A und B sind stochastisch unabhängig, wenn P(A∩B)=P(A)*P(B) gilt.
Wir wissen, dass P(A)=0,7 und dass P(A)*P(B)=0,28. Somit muss 0,28/0,7 P(B) sein, also P(B)=0,4. Jetzt können wir P(Ā)*P(B) berechnen, also 0,3*0,4. Das ist 0,12. Wir sehen aber, dass es 0,15 sein muss. Somit ist P(B) anhängig davon, ob A oder Ā eingetreten ist.
Einfacher erklärt: Sind die Wahrscheinlichkeiten nach A und nach Ā identisch? Nein, denn nach A folgt 0,4 und 0,6 und bei Ā folgt aber 0,5 und 0,5 und nicht noch einmal 0,4 und 0,6 (B ist abhängig von A). Die Ereignisse sind also stochastisch abhängig.