Boolesche Funktion vereinfachen?

Hallo hallo, gibt es hier zufällig jemanden der gut in Mathe ist?

Beim bearbeiten von Klausuraufgaben kam ich auf eine Boolesche Funktion welche ich nicht vereinfachen kann, leider hab ich keine Lösungen.

Die Funktion mit der Aufgabe: "Vereinfachen Sie den Funktionsterm so weit, wie möglich."

f (a , b , c)= (a+b)⋅((ab)'+c)((a '+c)' +b' )

Es wäre super wenn jemand Zeit und Lust hätte diese Aufgabe zu lösen ^^

Answer 1

[Rammstein53]

(a+b)·((ab)'+c)((a '+c)' +b' )

Wegen (ab)' = a' + b':

(a+b)·(a' + b' + c)((a ' + c)' + b' )

Wegen (a' + c)' = ac':

(a+b)·(a' + b' + c)(ac' + b')

(a+b)·(a'(ac') + b'(ac') + c(ac') + a'b' + b'b' + cb')

Wegen aa' = 0 und b'b' = b':

(a+b)·(ab'c' + ac' + a'b' + b' + cb')

b' beinhaltet a'b' und ab'c':

(a+b)·(b' + ac' + cb')

ab' + aac' + acb' + bb' + bac' + bcb'

Wegen aa = a und bb' = 0:

ab' + ac' + acb' + abc' + bc'

ab' + abc' + ac' + acb' + bc'

Daraus folgt die vereinfachte Form:

ab' + ac' + bc'

Answer 2

[mihisu]

Ich nehme mal an, dass ein Apostroph hier für eine Negation stehen soll. Da ich das so eher gewohnt bin, werde ich im Folgenden die Negation stattdessen mit einer Überstreichung markieren.

=== Mit Hilfe der von Rechengesetzen der boolschen Algebra umformen ===

Das könnte man dann beispielsweise folgendermaßen vereinfachen...

$f(a, b, c)=\left(a+b\right)\cdot\left(\overline{a\cdot b}+c\right)\cdot \left(\overline{\overline{a}+c}+\overline{b}\right)$

[Mit De-Morgan-Regel ist (ab)' = a' + b' und (a' + c) = a'' * c'.]

$f(a, b, c)=\left(a+b\right)\cdot\left(\overline{a}+\overline{b}+c\right)\cdot \left(\overline{\overline{a}}\cdot\overline{c}+\overline{b}\right)$

[Bei den linken beiden Klammern kann man ausmultiplizieren (Distributivität). Weiter rechts kann man a'' = a vereinfachen.]

$f(a, b, c)=\left(a\cdot\left(\overline{a}+\overline{b}+c\right)+b\cdot\left(\overline{a}+\overline{b}+c\right)\right)\cdot \left(a\cdot\overline{c}+\overline{b}\right)$

$f(a, b, c)=\left(a\cdot\overline{a}+a\cdot\overline{b}+a\cdot c+b\cdot\overline{a}+b\cdot\overline{b}+b\cdot c\right)\cdot \left(a\cdot\overline{c}+\overline{b}\right)$

[Es ist a * a' = 0 und b * b' = 0.]

$f(a, b, c)=\left(0+a\cdot\overline{b}+a\cdot c+b\cdot\overline{a}+0+b\cdot c\right)\cdot \left(a\cdot\overline{c}+\overline{b}\right)$

[0 fällt hier bei ODER-Verknüpfung bzw. Addition weg.]

$f(a, b, c)=\left(a\cdot\overline{b}+a\cdot c+b\cdot\overline{a}+b\cdot c\right)\cdot \left(a\cdot\overline{c}+\overline{b}\right)$

[Dann würde ich weiter ausmultiplizieren (Distributivität).]

$f(a, b, c)=\left(a\cdot\overline{b}+a\cdot c+b\cdot\overline{a}+b\cdot c\right)\cdot a\cdot\overline{c}+\left(a\cdot\overline{b}+a\cdot c+b\cdot\overline{a}+b\cdot c\right)\cdot \overline{b}$

$f(a, b, c)=a\cdot\overline{b}\cdot a\cdot\overline{c}+a\cdot c\cdot a\cdot\overline{c}+b\cdot\overline{a}\cdot a\cdot\overline{c}+b\cdot c\cdot a\cdot\overline{c}+a\cdot\overline{b}\cdot \overline{b}+a\cdot c\cdot \overline{b}+b\cdot\overline{a}\cdot \overline{b}+b\cdot c\cdot \overline{b}$

[Dann würde ich bei den einzelnen Summanden die Faktoren etwas umsortieren (Kommutativität).]

$f(a, b, c)=a\cdot a\cdot\overline{b}\cdot\overline{c}+a\cdot a\cdot c\cdot \overline{c}+\overline{a}\cdot a\cdot b\cdot\overline{c}+a\cdot b\cdot \overline{c}\cdot c +a\cdot\overline{b}\cdot \overline{b}+a\cdot \overline{b}\cdot c+\overline{a}\cdot \overline{b}\cdot b+\overline{b}\cdot b\cdot c$

[Dann kann man gleiche Faktoren zusammenfassen, also beispielsweise a * a = a zusammenfassen (Idempotenz). Und man kann das Komplementärgesetz anwenden, um beispielsweise c * c' = 0 zu vereinfachen, wobei dann (irgendwas) * 0 = 0 ist und (irgendwas) + 0 = (irgendwas) ist.]

$f(a, b, c)=\overbrace{a\cdot a}^{=a}\cdot\overline{b}\cdot\overline{c}+\underbrace{\overbrace{a\cdot a}^{=a}\cdot \overbrace{c\cdot \overline{c}}^{=0}}_{=0}+\underbrace{\overbrace{\overline{a}\cdot a}^{=0}\cdot b\cdot\overline{c}}_{=0}+\underbrace{a\cdot b\cdot \overbrace{\overline{c}\cdot c}^{=0}}_{=0} +a\cdot\overbrace{\overline{b}\cdot \overline{b}}^{=\overline{b}}+a\cdot \overline{b}\cdot c+\underbrace{\overline{a}\cdot \overbrace{\overline{b}\cdot b}^{=0}}_{=0}+\underbrace{\overbrace{\overline{b}\cdot b}^{=0}\cdot c}_{=0}$

$f(a, b, c)=a\cdot\overline{b}\cdot\overline{c}+a\cdot \overline{b}+a\cdot \overline{b}\cdot c$

[Da kann man dann a * b' ausklammern (Distributivität).]

$f(a, b, c)=a\cdot\overline{b}\cdot\left(\overline{c}+1+c\right)$

Bei der ODER-Verknüpfung mit 1 erhält man c' + 1 = 1 bzw. 1 + c = 1 (Extremalgesetz).

$f(a, b, c)=a\cdot\overline{b}\cdot 1$

Schließlich hat man dann am Ende...

$f(a, b, c)=a\cdot\overline{b}$

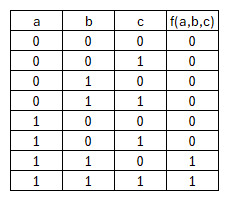
=== Alternativ: Mit Hilfe einer Wertetabelle ===

Mit Hilfe einer Wertetabelle...

... kann man...

$f(a, b, c) = a\cdot \overline{b}\cdot \overline{c} + a\cdot \overline{b}\cdot c$

... als disjunktive Normalform finden, welche sich dann schnell und einfach weiter zu...

$f(a, b, c) = a\cdot \overline{b}$

... vereinfachen lässt.

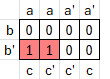
Bzw. wenn man die Wertetabelle in Form eines KV-Diagramms auswertet...

... kann man auch...

$f(a, b, c) = a\cdot \overline{b}$

... als Ergebnis ablesen.

Comments

[IchHabFragen186]

Danke dir, dass du dir die Zeit genommen hast!

Answer 3

[MagicalGrill]

Lösungsweg: Nutz halt die Rechenregeln, um die ganzen Klammern aufzulösen.

Bsp: (ab)' = a' + b' [DeMorgan].

Dann kannst du die ersten beiden Klammern ausmultiplizieren [Distributivgesetz], dabei fallen dann ein paar Terme weg wie z.B. aa' = 0.

Zur Kontrolle: Ich komme letztendlich auf f(a,b,c) = ab'.