Betragsgleichung, wie Fallunterscheidung machen?
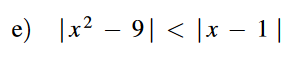

Wie ist die erste Lösung möglich?
Da überprüfen wir doch, ob x²-9>=0 und x-1<0 ist, also x>=3 und x<1, aber wie soll x größer gleich 3 und gleichzeitig kleiner als 1 sein? Ich glaube, ich habe dieses Thema falsch verstanden und gelernt.
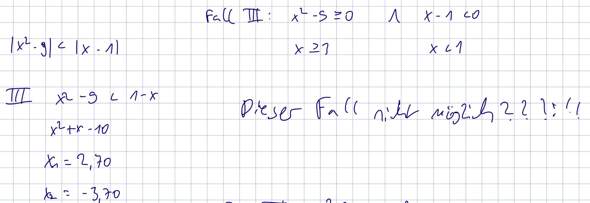
2 Antworten
Die erste lösung ergibt sich aus der Fallunterscheidung für die Betragsgleichung, Du hast Recht, dass zunächst x²-9>=0 und x-1<0 überprüft werden müssen, Hier liegt der Fehler in deiner rechnung Für x²-9>=0 ergibt sich x >= 3 oder x <= -3, Für x-1<0 ergibt sich x < 1 Wenn wir diese beiden Bedingungen kombinieren, erhalten wir -3 <= x < 1 als lösungsmenge, Also ist x größer gleich -3 und gleichzeitig kleiner als 1 möglich Du hast das Thema nicht falsch verstanden, es war nur ein kleiner Fehler in deiner rechnung
Da überprüfen wir doch, ob x²-9>=0 und x-1<0 ist, also x>=3 und x<1
x² - 9 ≥ 0 wird nicht nur durch x ≥ 3 gelöst, sondern auch durch x ≤ -3.
[Setze beispielsweise mal x = -4 ein. Du wirst erkennen, dass dies eine Lösung der Ungleichung x² - 9 ≥ 0 ist, obwohl dabei nicht x ≥ 3 gilt.]
Und der Bereich mit x ≤ -3 überschneidet sich dann sehr wohl mit dem Bereich x < 1. [Der Schnittbereich besteht dann aus allen Zahlen x mit x ≤ -3. Und die angegebene Lösung x₁ liegt in diesem Schnittbereich.]
Naja, es geht nicht unbedingt ums „potenzieren“ mit einer negativen Zahl. [Außerdem wird ja auch nicht „mit“ einer negativen Zahl potenziert, da der Exponent 2 ja positiv ist, sondern es wird eine negative Zahl potenziert (und das mit einem geraden Exponenten).]
Ich würde das eher so sehen... Für reelle Zahlen x ist
x² - 9 ≥ 0
äquivalent zu
x² ≥ 9
und des Weiteren äquivalent zu
|x| ≥ 3.
Dann kann man eine Fallunterscheidung durchführen...
- Für x ≥ 0 ist |x| = x und man erhält x ≥ 3.
- Für x < 0 ist |x| = -x und man erhält -x ≥ 3. Dann erhält man nach Multiplikation mit -1, wobei sich das Relationszeichen dann (entsprechend dem Inversionsgesetz) umdreht, die Ungleichung x ≤ -3.
-------------
Ansonsten könnte man es auch so sehen...
Die reellen Zahlen, die x² - 9 ≥ 0 erfüllen, sind genau die reellen Zahlen, die nicht x² - 9 < 0 erfüllen. Die Ungleichung x² - 9 < 0 ist äquivalent zu x² < 9 bzw. zu |x| < 3 bzw. äquivalent zu -3 < x < 3. Wenn man diesen Bereich nun aus dem reellen Zahlenstrahl entfernt bleibt auf der negativen Seite ein Intervall von -∞ bis einschließlich -3 (also x ≤ -3) und auf der positiven Seite ein Intervall von einschließlich 3 bis +∞ (also x ≥ 3) übrig.
Naja, ich würde nur 4 Fälle unterscheiden...
Da x² - 9 und x - 1 stetig auf ganz ℝ sind und nur an ihren Nullstellen das Vorzeichen wechseln können, sind eigentlich nur die Nullstellen x = -3 und x = 3 bzw. x = 1 als Übergänge interessant. Ich würde dementsprechend die folgenden Fälle unterscheiden...
- x < -3 [In diesem Fall wird die Ungleichung zu x² - 9 < -(x - 1).]
- -3 ≤ x < 1 [In diesem Fall wird die Ungleichung zu -(x² - 9) < -(x - 1).]
- 1 ≤ x < 3 [In diesem Fall wird die Ungleichung zu -(x² - 9) < x - 1.]
- 3 ≤ x [In diesem Fall wird die Ungleichung zu x² - 9 < x - 1.]
----------
Bzw. kann man vielleicht besser erkennen, dass diese Fälle reichen, wenn man x² - 9 als (x - 3) ⋅ (x + 3) schreibt und |x² - 9| < |x - 1| entsprechend in |x - 3| ⋅ |x + 3| < |x - 1| umformuliert.
===========
Aber ansonsten, wenn man nach und nach die Beträge einzeln mit Fallunterscheidung auflöst... Ja, es können recht viele Fälle werden. Dann muss man die einfach ordentlich nummerieren und sauber aufschreiben, dass man nicht durcheinander kommt.
Aber x² - 9 ≥ 0 würde ich auch normalerweise gar nicht so ausführlich auflösen, sondern direkt schreiben, dass das äquivalent zu „x ≤ -3 oder x ≥ 3“ ist. Das war eher zur genaueren Erklärung für dich, warum das so ist.
"x ≥ 3 gelöst, sondern auch durch x ≤ -3" wird hier die Ungleichung umgekehrt, da wir mit einer negativen Zahl potenzieren, um zur ursprünglichen Wurzelfunktion zu kommen?