Ballwurf Geschwindigkeit?
Ein Schüler wirft einen Ball 42m weit. Ermitteln Sie daraus die Geschwindigkeit, mit der der Schüler den Ball mindestens abgeworfen hat.
Wahrscheinlich ist das ein schräger Wurf
Die Strecke ist 42m weit
Gravitationskraft beträgt 9,81
Wie muss ich jetzt weiter vorgehen?
Danke
5 Antworten
ausgehend von Brainchilds Hinweisen , musst du von alpha = 45° ausgehen , und solltest dann diese Formel nach v umstellen:
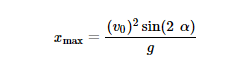
wobei x max = 42 ist
Formel von hier
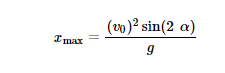
Natürlich ist das ein schräger Wurf. Bei einem waagerechten Wurf kämest du mathematisch auf eine Weite von exakt 0 m. Bei einem senkrechten ebenso.
Den optimalen Abwurfwinkel kennt man, schlägt ihn nach oder berechnet ihn, was naürlich am aufwendigsten ist.
Jedenfalls musst du den Abwurfwinkel in eine senkrechte und eine waagereche Komponente zerlegen, Sinus und Cosinus. Nach dem Satz des Pytharoras ergibt sich s-Komp² + w-Komp² = Wurfgeschwindigkeit².
Mit der senkrechten Geschwindigkeitskomponente ergibt sich die Wurfzeit, gem. v=a*t, also t=v/a, das Ganze mal 2 weil der Ball steigt und dann sinkt, also t=2v/a.
Mit der Zeit errechnest du dann die Wurfweite gem. s=v*.
So viel als Anregung. Mathe ist über 40 Jahre her bei mir. Ich würd's wohl noch hinkriegen, aber ich lasse dir den Vortritt. Vielleicht gibt's das aber schon vorgekaut. Brainchilds Link bin ich nicht gefolgt, aber er sieht erfolgversprechend aus.
siehe Physik-Formelbuch,was man privat in jedem Buchladen bekommt.
Kapitel,schräger Wurf
maximale Wurfweite unter einem Abwurfwinkel von (a)=45°
smax=Vo²/g*sin(2*a) mit sin(2*45°)=1
smax=Vo²/g
Vo=Wurzel(s*g)=Wurzel(42m*9,81 m/s²)=20,298.. m/s
Zu wenige Angaben. Allgemeine und spezielle Fälle:
https://de.wikipedia.org/wiki/Wurfparabel#Wurfparabel_mit_Luftwiderstand
Tipp: Da es heißt: "Ball mindestens abgeworfen" musst du den Abwurf-Winkel nehmen, bei dem man am weitesten kommt (45°). Und gehe mal von keinem Luftwiderstand aus.
Du musst wissen, aus welcher Höhe der Ball abgeworfen wurde. Daraus ergibt sich eine Falldauer bis zum Boden.
Mit dieser Zeit kannst du berechnen, wie schnell der Ball (Vernachlässigung des Luftwiderstandes vorausgesetzt) geworfen werden muss, um in "x" Sekunden 42 m weit zu kommen.
Ja deswegen komm ich grad nicht weiter im Text stehen nur diese Angaben :/.