3 Äquivalenzpunkte bei Titration von Phosphorsäure mit NaOH- Was gilt und wo?

Also beim 1, gilt ja

n_S = n_B und c_sV_s = c_BV_B

Also stoffmenge Base, hier NaOH, gleich Stoffmenge Säure, hier H3PO4 mit folgender Reaktion

H₃PO₄ + NaOH ⇌ H₂PO₄^- + Na⁺ + H₂O

jetzt ist ja phosphorsäure eine dreiprotonige säure, d.h. ich brauche 3 mal NaOH um ein Phosphorsäuremolekül zu eliminieren, doch wir bringe ich das in die gleichung bzw. reaktion ein? und warum sinkt die leitfähigkeit? Wasser liegt ja meist nicht dissoziiert vor, also nicht als H^+ und OH^(-),sondern eben also Wasser H_2O Deswegen?

ab dem 2. Äquivalenzpunkt steigt die leitfähigkeit wieder

H₂PO₄^- + 2NaOH ⇌ HPO₄^2- + 2H₂O + 2Na⁺

mit dieser reaktion, doch warum? Weil da mehr Ionen sind bzw. HPO_4^(2-) eine schwache säure ist?

und beim 3. Äquivalenzpunkt steigt sie ja auch, bloß stärker

HPO₄^2- + NaOH ⇌ PO₄^3- + H₂O + Na⁺  

ist die begründung weil PO_4^(3-) noch schwächer ist?

Danke vielmals und würde mich sehr freuen, wenn jemand die gleichungen noch kontrollieren könnte.

lg

Answer 1

[wonno93]

Indiachinacook hat es schon gut ausgeführt, bereits beim zweiten Knick ist der Sprung kleiner. Beim dritten eben kaum ersichtlich, da das Gleichgewicht sich viel eher bei der dritten Protonierung auf der linken Seite bleibt ,da HPO4 bereits 2 fach Negativ geladen ist und daher "ungerne" ein weiteres seiner Protonen (H+) für die Reaktion zur Verfügung stellt. Daher ist diese Reaktion in der Praxis fast nur unvollständig zu erzeugen.

Sie ist für diese Methode wegen der viel zu geringen zu messenden Differenzen nicht wirklich geeignet für eine Quantitative Bestimmung. Die anderen beiden Äquivalenzpunkte sollten auch ausreichen.

Mir ergibt es sich nicht ganz warum oben nur die erste Protonierungsstufe abgebildet ist, aber in der zweiten Reihe dann die Zusammengefasste Stufe aus den ersten beiden genommen worden ist. So ergibt sich es das die zweite Stufe nicht stimmt, links 4 H+, rechts nur 3.

Comments

[aabbcc1]

Hallo,

danke, stimmt. Wüsstest Du, wie ich das ausgleichen könnte bzw. was meinst du mit der zusammengefasste Stufe?

danke nochmal, hat sehr geholfen.

[wonno93]

@aabbcc1

H2PO4 - + 1 NaOH ⇌ HPO4 2- + 1 H2O + Na+, ich würde es ganz einfach halten

Ich dachte du wolltest (wegen 2 Mol NaOH) die erste und zweite Protonierung in eine Stufe packen ... aber es geht auch nicht auf da bereits H2PO4 als Edukt in der zweiten Stufe steht. Mich hat die mittlere Stufe jedenfalls verwirrt.

[aabbcc1]

@wonno93

Danke, doch geht da nicht die Information verloren, dass man eben 2 Moleküle NaOH benötigt, um ein Molekül des HPO4 2- zu neutralisieren?

[wonno93]

@aabbcc1

Meintest du nicht von der Phosphorsäure zu HPO4 2- zu neutralisieren. Das meinte ich mit "Zusammengefasst".

Nur im selben Verhältnis ist die Gleichung bei diesen Edukten an Atomanzahl und Ladungen ausgeglichen. Um das Vorgehen zu veranschaulichen halte ich ausreichend Edukte und Produkte gegenüber zu stellen und ihre Leitfähigkeit gegenüber einander zu stellen.

Ich bin grade echt am grübeln worauf du hinaus möchtest.

Answer 2

[Picus48]

Dazu habe ich das hier gefunden: http://unterrichtsmaterialien-chemie.uni-goettingen.de/material/9-10/V9-323.pdf

Dabei sinkt die Leitfähigkeit bis zum ersten Äquivalentpunkt, da die Hydroxoniumionen, die eine gute spezifische Leitfähigkeit haben, mit den Hydroxydionen zu elektrisch neutralem Wasser reagieren und die entstandenen Ionen H₂PO₄^- und Na⁺ eine spezifisch schlechtere Leitfähigkeit haben. Im Verlauf der weiteren Zugabe von NaOH steigt die Leitfähigkeit wieder an.

Die Leitfähigkeit ist nicht nur abhängig von der Anzahl der Ladungsträger (Konzentration) sondern auch von der Beweglichkeit der Ionen, wobei kleinere Ionen in der Tendenz eine höhere Beweglichkeit und spezifische Leitfähigkeit aufweisen.

Woher ich das weiß: Studium / Ausbildung

Answer 3

[indiachinacook]

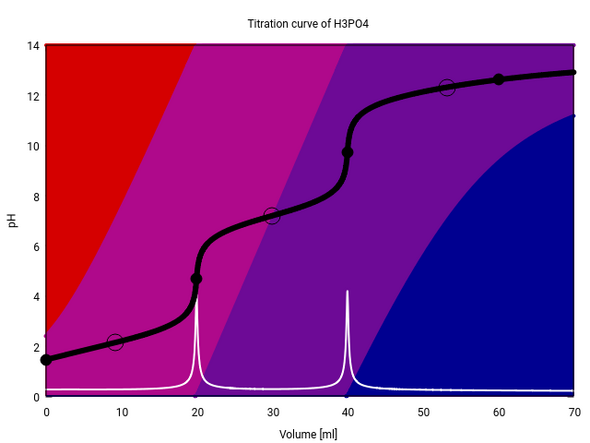
Ich habe kein Programm, mit dem ich eine Leitfähigkeitstitration simulieren kann (ob­wohl, hmm, eigentlich, hmm, habe ich schon einen Plan was ich morgen mache?). Deshalb zeige ich Dir die potentiometrische Titration von H₃PO₄ mit NaOH und pH-Elektrode:

Du siehst den pH-Wert als schwarze Kurve (die weiße ist die Ableitung davon), und die Hintergrundfarben geben an, wieviel freie Säure (rot) bzw. die Anionen (in Violett- bzw. Blautönen) in der Suppe herumschwimmen. Titriert wurden 20 ml einer 0.1 mol/l H₃PO₄ mit 0.1 mol/l NaOH, die drei Äquivalenzpunkte liegen also bei 20, 40 und 60 ml Verbrauch.

Bei den ersten beiden Äquivalenzpunkten springt der pH, beim dritten nicht mehr. Folglich sind nur zwei sichtbar, der dritte geht unter (das liegt daran, daß PO₄³⁻ [blau] stark hydrolysiert, also im Gleichgewicht mit ziemlich viel HPO₄²⁻ [blauviolett] steht und die Lösung niemals zu 100% dominiert). Die Leitfähigkeit hängt ja auch sehr stark vom pH ab, und deshalb wirst Du auch konduktometrisch vom dritten ÄP nichts sehen können: Keine pH-Änderung ⟹ keine Leitfähigkeitsänderung.

Die ersten beiden Äquivalenzpunkte sollten Dir aber jeweils einen sichtbaren Knick in der Leitfähigkeit ergeben. Am ersten gilt n(Base)=n(Säure), und am zweiten natürlich n(Base)=2⋅n(Säure).

Ich würde annehmen, daß die Leitfähigkeit zwischen 0 und 20 ml einigermaßen kontinuirlich sinkt (Verlust von H₃O⁺), dann einen Knick hat und sich bis 40 ml nur wenig ändert (leichter Anstieg durch die Na⁺-Ionen, leichter Abfall durch den Verlust der letzten paar H₃O⁺), und dann bei der 40 ml wieder knickt und danach ansteigt, weil sich OH⁻ bildet, das auch passabel leitet, wenn auch nicht so gut wie H₃O⁺.

Woher ich das weiß: Studium / Ausbildung – Chemiestudium mit Diss über Quanten­chemie und Thermodynamik

Comments

[aabbcc1]

Danke, ich habe eine neue Frage gestellt und würde mich sehr freuen, wenn Du kurz vorbeischauen könntest.

Lg