Worin liegt der wesentliche Unterschied zwischen den magnetischen und den elektrischen Kräften?
Wenn ich im Internet recherchiere, bekomme ich oft zu lesen, dass der Unterschied darin liegt, dass die Anziehungskraft von Magneten auf die Pole gerichtet ist. Dahingegen weisen die Kräfte elektrischer Körper aus dem Zentrum heraus isotrop auf jeden Punkt ihrer äußersten Oberfläche.
Die oft wiederkehrende Wiederholung zeigt mir, dass hier stur auswendig Gelerntes wiedergegeben wird, denn es findet immer dasselbe abstrakte Schema Anwendung, doch das Wesen dieses Unterschieds findet nur wenig Aufmerksamkeit, obwohl es in den Illustrationen klar in den Vordergrund rückt.
So ähnlich und noch viel komplexer kannst du diverse Erklärungen finden, die dein Unwissen eher vertiefen als über den Unterschied aufzuklären. Abgesehen davon, dass manche Vorgänge auch noch völlig falsche Vorstellungen assoziieren, weil sie tatsächlich falsch dargestellt werden, was allein dem Showeffekt einer Animation geschuldet ist, aber keinesfalls einer wissenschaftlich plausiblen Erklärung nützt.
So kann man alles zwar als Eselsbrücke gut verstehen, aber damit kann man nicht auf redundante Zusammenhänge schließen. Also:
Hast du vielleicht eine einfachere, plausiblere Erklärung, worin der Unterschied zwischen den magnetischen Kräften und den elektrischen liegt?
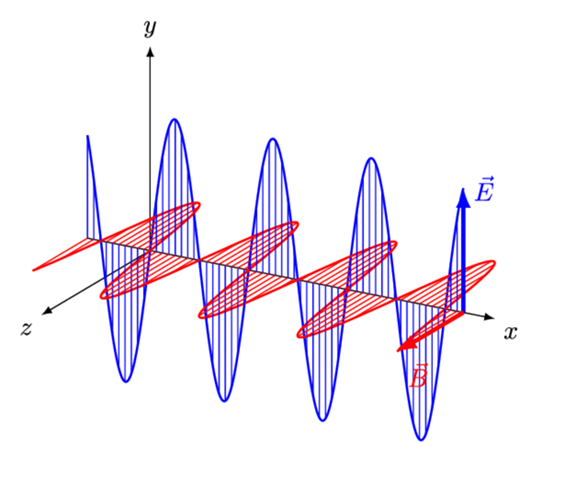
Denn z.B. die grafischen Erklärungen für eine elektromagnetische Welle nutzen diesen eklatanten Unterschied gerne für ihre Illustrationen – siehe z.B. Wikipedia und zwar auf ganz besonders irreführende Weise.
Hier also nur die nicht animierte Darstellung:

Nachtrag: Offensichtlich wäre z. B., dass jeder versucht, eine gleichschenklige rechtwinklige Beziehung zu zeichnen, obwohl es kleine gibt.
Um dieses nun noch einmal verbessert zu erklären, habe ich jetzt noch eine zusätzliche Erklärung als eigene Antwort verfasst.
3 Antworten
Man fasst elektrische und magnetische Kräfte, Felder etc. üblicherweise zu elektromagnetischen Kräften, Feldern etc. zusammen, weil man sie sehr leicht als Teilphänomene dieser Zusammenfassung darstellen kann.
Der Unterschied besteht darin, dass wir elektrische "Monopole" kennen, aber (bisher?) keine magnetischen.
Magnetische und elektrische Dipole verhalten sich völlig analog (ebenso Quadrupole, Oktopole und höhere Multipole).
Wie ich hier nun feststelle, ist wohl niemand von den Experten in der Lage (oder willens), zu erkennen, wonach ich fragte, und so mancher meint sogar, meine Zusatzerklärung sei irgendwas aus dem Zusammenhang Gezogenes, in den Raum Geworfenes. Daher versuche ich nun noch einmal im Detail näher zu erklären, wo ich das Problem einer „gleichschenklig rechtwinkligen" Beziehung sehe. Natürlich will ich auch gerne für die, die nicht so schnell begreifen, auch etwas tiefergehend beschreiben, was genau ich daran denn falsch finde und wo dies im Widerspruch zur etablierten Physik steht.
Denn nicht jedem ist es von Gott gegeben, die Dinge mit dem eigenen Verstand zu durchdringen, besonders dann nicht, wenn es nicht so, wie ich es beschreibe, in den Lehrbüchern zu finden ist.
Also das Wesentliche meiner Frage ist, dass die elektrischen und magnetischen Kräfte rechtwinklig, also orthogonal bzw. 90° zueinander stehen,
Also nach einigen Recherchen fand ich heraus, dass das mit den 180 ° nicht stimmen kann. Daher betrachte die alte Feststellung vorerst als Blödsinn meinerseits.
Was diese 180° betrifft, füge ein Zitat aus den Pfründen der Uni Ulm hinzu und gehe davon aus, dass jeder bemerkt, dass die Wirkungsrichtungen einerseits unterschiedlich und andererseits nur auf eine Dimension bezogen sind und daher die Richtungen nur um 180° gedreht werden können.
Die Anziehungskraft von Magneten ist auf die Pole gerichtet, die elektrischer Körper auf jeden Punkt der Oberfläche. --> Theorie des Magnetismus und der Elektrizität
Wenn man nun das von mir erwähnte Beispiel der Wikipedia betrachtet und sich besonders die verlinkte Animation davon ansieht. Dann sollte man erkennen, dass beide Wirkungsrichtungen in die gleiche Richtung zeigen – also nicht 180° gegeneinander verlaufen.

Ferner haben die dargestellten Kräfte auch identische Amplituden zum gleichen Zeitpunkt, denn die eigentliche X-Achse ist keine räumliche Dimension, sondern stellt eine zeitlich orientierte Achse dar, wo jeder Punkt die gleichzeitige Gegenwart kennzeichnet.
Daher haben zu jedem Zeitpunkt die beiden Amplituden die gleiche Länge und daher betonte ich extra den Begriff „gleichschenklig”, weil es keine gleichzeitig gleichen Schenkel der rechtwinkligen Anordnung geben kann. Denn die Bewegungsrichtungen sind um 180° gedreht, womit ein umgekehrt proportionales Verhältnis die Schenkellänge bestimmt.
Die Zusammenhänge sind aber von trigonometrischer Natur und es wird damit kein räumlicher Verlauf beschrieben, sondern ein zeitlicher. Also, letztendlich stehen sich die mathematischen Sinus- oder Kosinuswerte ergänzend um 90° phasenverschoben gegenüber, womit sich eine zeitliche Strecke beschreibt und nicht eine räumliche.
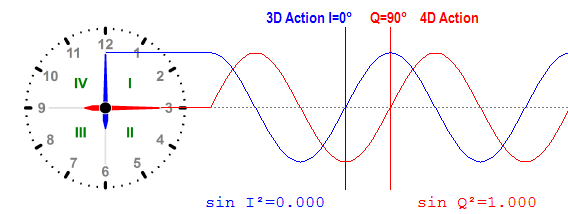
Um nun die räumliche 90° -Eselsbrücke besser zu assoziieren, wäre es besser, einen zeitlich orientierten 90°-Abstand einer Uhr zu zeichnen, die die Phasenverschiebungen deutlich plausibler in den Vordergrund stellt. So dass man erkennt, dass zu keinem Zeitpunkt die elektrische oder die magnetische Kraft die gleiche Amplitude haben kann.

Dies ist ein Auszug aus einem animierten GIF, welches leider nicht von gutefrage.de dargestellt werden kann. Wenn du dem Link folgst, dann erscheint eine animierte Darstellung eines zeitlichen Verlaufs.
So ging ich nun naiverweise in der Hoffnung schwanger, dass man eigentlich davon ausgehen kann, dass man hier bei gutefrage.de danach fragen könnte, was denn nun richtig oder was falsch sei an meinem Vergleich mit der Wikipedia, ohne gleich von den selbsternannten Experten angepöbelt zu werden.
Denn die animierte Darstellung der Wikipedia zeigt zwei gleiche Amplituden zur gleichen Zeit und beide Wirkungsrichtungen verlaufen auch in die gleiche Richtung. Ich erwarte nämlich, dass die magnetischen Kräfte zum zentralen Punkt hin verlaufen sollten, oder sehe ich das falsch?
man kann nach dem dritten Absatz schon zu lesen aufhören, da du scheinbar entweder
- keien Ahnung von Physik hast oder
- provozieren willst.
Du kritisierst etwas, das seit mehr als hundert Jahren als gesichert etabliert ist und willst uns mit lächerlichstenen Argumenten überzeugen, dass hier etwas faul sein müsse?
Mal im Ernst: Tut es dir nicht leid um deine Zeit, die du hier sinnlos vergeudest? Ja, die Sätze sind grammatikalisch richtig, aber deswegen ergeben sie noch lange keinen Sinn. Du machst dich hier nur lächerlich: echte Genies haben was drauf und können auch erklären, was sie meinen und konkret aufzeigen, wo in der Physik ein mögliches Problem ist. Du kannst das nicht mal im Ansatz und bist Lichtjahre davon entfernt, auch nur in hömöopathischen Dosen ernst genommen zu werden.
doch das Wesen dieses Unterschieds findet nur wenig Aufmerksamkeit, obwohl es in den Illustrationen klar in den Vordergrund rückt.
Vielleicht könntest du uns ja erleuchten, indem du das "Wesen" selbst beschreibst und uns mit deinen Worten mal erklärst, was an dem gezeigten Bild oder den sonst animierten Darstellungen so klar in den Vordergrund rückt, welches deiner Meinung nach aber nie oder kaum erwähnt wird.
Man lernt nie aus, also bitte, ich bin gespannt.
Das ist keine Antwort auf die Frage von AMG38 - oder ? Du wirfst irgendwas aus dem Zusammenhang gezogenes in den Raum und wir sollen drauf argumentieren? Erkläre im doch mal im Detail wo du hier das Problem einer "gleichschenkelig rechtwinkeligen Beziehung" zu sehen glaubst und dann bitte auch gleich, was genau du daran falsch findest und wo dies im Widerspruch zur etablierten Physik steht, die du angeblich widerlegt hast. *LOL*
Na ja, offensichtlich wäre z.B., dass jeder versucht eine gleichschenklige rechtwinklige Beziehung zu zeichnen, obwohl es kleine gibt.