Zeigen Sie, dass f unendlich viele Extrema besitzt?
Ich rechne gerade zur Klausurvorbereitung Aufgaben. Eine neue davon:
Zeigen sie, dass f unendlich viele lokale Extrema beiderlei Typs besitzt.
Die Ableitung ist kein Problem:
Mein Ansatz:
Ich muss zeigen, dass f' unendlich viele Nullstellen besitzt. Das dürfte durch sin/cos nicht schwer sein, ich habe aber keine Ahnung wie ich das machen muss, da wir immer nur den Nullstellensatz anwenden und durch einsetzen dann nur Intervalle herausbekommen, in denen eine Nullstelle liegen muss. Wie zeige ich jetzt, dass es unendlich viele gibt? Und wie zeige ich im Anschluss, dass es auch unendlich viele Extrema gibt?
2 Antworten
Dein Ansatz ist im Grunde richtig. Du musst nur noch zeigen, dass die Ableitung aller Pi/2 eben diese Nullstellen hat und dieser sich nicht mit x ändert.
(Dazu ggf. noch den Wertebereich begründen!)
Da auch die erste Ableitung eine trigonometrische Funktion ist, hat diese Funktion unendlich viele Nullstellen mit VZW. Somit auch unendlich viele Extrema.
Da diese Gleichung eine Periode von \pi/2 hat gibt es unendlich viele Nullstellen mit VZW, wie auch die Grafik zeigt:
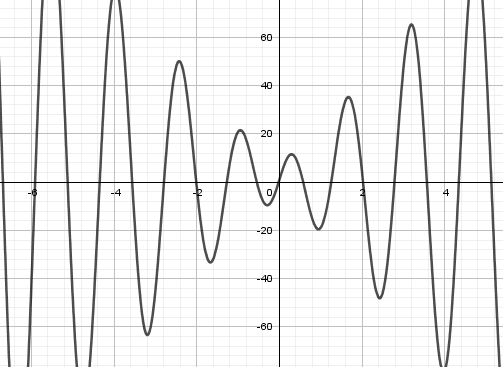
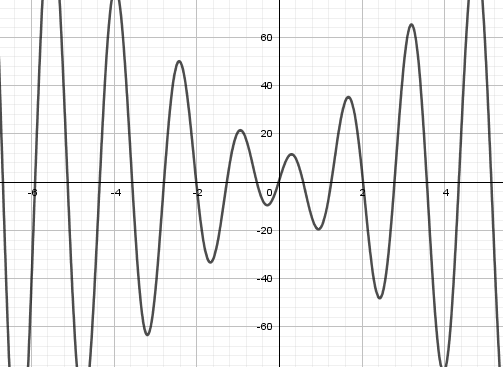
Da diese Gleichung eine Periode von \pi/2 hat
Wie genau bist du darauf gekommen? Die Grafik hilft schon gut, aber in der Klausur habe ich ja nicht einmal einen Taschenrechner. Ich darf das mit Sicherheit auch nicht einfach nur begründen, sondern muss irgendwie ausrechnen, dass die Periode pi/2 ist. Ich weiß nicht wie ich das machen kann.
Die Periode berechnet sich aus p=2 * \pi / b. b ist die Zahl, die beim sin, cos bzw. tan in der Klammer vor dem x steht. In deinem Beispiel ist das eine 4, somit p=2 * \pi / 4 = \pi / 2.