Wie setze ich die Funktion: f(x)=cos(x²)⋅2 = 0?

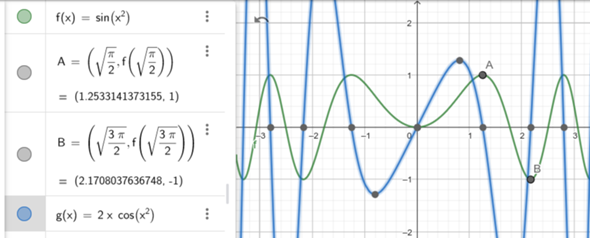
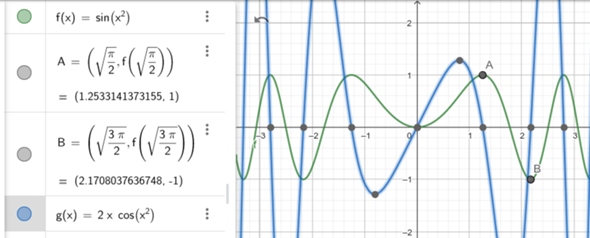
Hey ich habe eine Rechnung bekommen. Und zwar muss ich die Extrempunkte der Funktion f(x)=sin(x²) im Intervall (-2,5;2,5) berechnen. Dafür habe ich jetzt auch die 1. Ableitung durch die Kettenregel gebildet, aber jetzt weiß ich nicht wie ich die abgeleitete Funktion =0 setzten kann. Könntet ihr mir vielleicht eine Erklärung geben wie man dies berechnet?

Answer 1

[gauss58]

f(x) = sin(x²)

f'(x) = 2 * x * cos(x²)

0 = 2 * x * cos(x²)

Hier hilft der Satz vom Nullprodukt: Ein Produkt ist gleich Null, wenn einer der Faktoren Null ist.

Untersuche also, wann 2 * x gleich Null ist und wann cos(x²) gleich Null ist.

Answer 2

[evtldocha]

Wie setze ich die Funktion: f(x)=cos(x²)⋅2 = 0?

Die Ableitung von f(x)= sin(x²) lautet:

$f'\left(x\right)=2x\cdot\cos\left(x^2\right)$

Satz vom Nullprodukt

$\left(1\right)\ 2x\ =\ 0\ \Leftrightarrow x=0$ $\left(2\right)\ \cos\left(x^2\right)=0\ \Leftrightarrow x^2=\left(2k-1\right)\cdot\frac{\pi}{2}\ \ \ k\ \in\mathbb{N}^+\$

Aus (2) ergeben sich:

k=1:

$x_{2/3}=\pm\sqrt{\frac{\pi}{2}}$

k=2:

$x_{4/5}=\pm\sqrt{\frac{3\pi}{2}}$

k=3 liegt bereits außerhalb des Intervalls [-2,5; +2,5]

$|\pm\sqrt{\frac{5\pi}{2}}|\approx2,8\ >|\ \pm\ 2,5|$

Skizze: