Mathematik Ableitung arcsin(x)?

Die Ableitung von sin'(x) ist cos(x) (hier in rot markiert)
cos(x) wird jetzt umgeschrieben zu:
cos²(x) = 1 - sin²(x) | Wurzel
cos(x) = Wurzel(1 - sin²(x))
Jetzt steht hier im Nenner:
Wurzel(1 - sin²(x)) Jetzt müsst man das arcsin x für x einsetzen
"Bei 1 kann man das arcsin x nicht einsetzen"
allerdings bei -sin²(arcsin x)
Fkt und Umkehrfkt fressen sich auf, weshalb sin(arcsin x) = x ergibt
Durch das ² ensteht, dass x². Deshalb steht jetzt im Nenner
Wurzel(1 - x²).
In der Abbildung steht x ist Element ]-1,1[
Sind hier die eckigen Klammern richtig rum gesetzt?
Müsste es nicht normal x ist Element [-1,1] sein?
Was ist deine Frage?
Jetzt steht hier im Nenner:
Wurzel(1 - sin²(x)) Jetzt müsst man das arcsin x für x einsetzen
"Bei 1 kann man das arcsin x nicht einsetzen"
Das ist keine Frage, sondern Aussagen.
Du weißt was gemeint ist. Also!
Nein, weiß ich nicht. Du schreibst
"Bei 1 kann man das arcsin x nicht einsetzen"
Ich weiß nicht einmal was du mit "1" meinst. In deinem Bild taucht keine "1" auf. Also!
Steht doch dort:
cos(x) wird umgeschrieben
cos²(x) = 1 - sin²(x) | Wurzel
cos(x) = Wurzel(1 - sin²(x))
Diese 1 meine ich: Ursprünglich cos(arcsin x)
Wurzel(1 - sin²(x) für cos
3 Antworten
Ist unklar, warum aus sin²(arscin(x)) im Folgenden x² wird?
sin(arcsin(x))=x
sin²(arcsin(x))=sin(arcsin(x))*sin(arcsin(x))=x*x=x²
zu Deiner Ergänzung: -1 und 1 müssen ausgeschlossen werden, also ]-1;1[ ist richtig, denn mit x=-1 bzw. x=1 wird der Nenner Null (und bei Werten außerhalb dieses Intervalls würde der Term unter der Wurzel negativ werden)
Das Argument von cos heißt von vornherein nicht x, sondern arcsin(x), daher folgt aus cos(arcsin(x)):
sin²(arcsin(x))+cos²(arcsin(x))=1
<=> cos²(arcsin(x))=1-sin²(arcsin(x))
<=> cos(arcsin(x))=Wurzel(1-sin²(arcsin(x))) und das ist dann Wurzel(1-x²).
In Ordnung. Das wollte ich wissen! Vielen Dank
In der Abbildung steht x ist Element ]-1,1[
Sind hier die eckigen Klammern richtig rum gesetzt?
Müsste es nicht normal x ist Element [-1,1] sein?
Ja, sind richtig.
Setzt du nämlich x = ±1 ein, steht im Nenner eine Null, was nicht definiert ist.
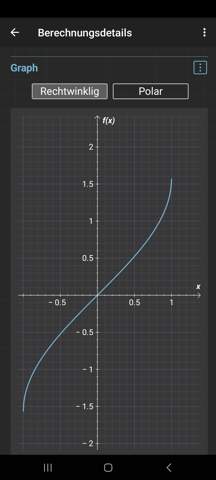
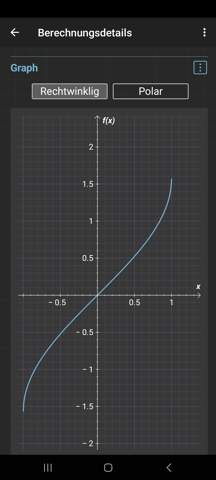
Hier siehst du, dass die Steigung an den Stellen ±1 sehr schnell stark ansteigt bis es nicht mehr definiert ist. Das findest du dann auch in der Umkehrfunktion wieder.
Ok. Danke.
hier steht zuvor im Nenner
cos(arcsin(x) das cos wird zu Wurzel (1 - arcsin²(x)) umgeformt, also müsste darstehen
Wurzel([1- sin²(x)] (arcsin x)
Weil ursprünglich hatte ich cos(arcsin(x)
Am Ende steht nicht da
Wurzel(1(arcsin x) - sin²(arcsin x)),
weil ich in die 1 arcsin(x) nicht einsetzten kann.
Jetzt verständlich?
Wie wo was?
arcsin(x) ist das Argument von cos(x). Bedeutet: Dort steht nicht cos(x) * arcsin(x), sondern cos( arcsin(x) ).
Anders formuliert. Wir können z := arcsin(x) setzen. Dann steht dort cos(z). Das ist das gleich wie
cos(z)
= √(1–sin²(z))
= √(1–sin(z)*sin(z))
= √(1–sin(arcsin(x))*sin(arcsin(x)))
= √(1–x*x) = √(1–x²)
"Bei 1 kann man das arcsin x nicht einsetzen"
Hier wird nicht arcsin(x) eingesetzt, sondern, wie es da steht, der trigonometrische Pythagoras verwendet, also
sin(x)^2 + cos(x)^2 = 1, oder eben
cos(x) = Wurzel( 1 - sin²(x)^2 )
Jetzt auf beiden Seiten arcsin(x) für x. Für die 1 muss man nichts "einsetzen".
cos(x) = Wurzel(1 - sin²(x))
Jetzt steht hier im Nenner:
Wurzel(1 - sin²(x)) Jetzt müsst man das arcsin x für x einsetzen
"Bei 1 kann man das arcsin x nicht einsetzen"
allerdings bei -sin²(arcsin x)
Sehe ich dies richtig?