Wie löse ich das mit einer zeichnung?
Ich hab diese Aufgabe bekommen und weiß nicht wie ich diese mit einer Zeichnung lösen soll : Eine Last von 20 kg hängt an einem Kabel, das durch ihr Gewicht durchhängt. Das Kabel bildet links und rechts von der Last jeweils einen Winkel von 60 Grad zur Vertikalen, sodass der Gesamtwinkel zwischen den beiden Seilhälften am Punkt, an dem die Last hängt, 120 Grad beträgt. Bestimme die Kraft, die in jeder Hälfte des Kabels wirkt, um das Gewicht zu tragen.
2 Antworten
Du zeichnest zuerst den Knotenpunkt der drei Seile in die Mitte vom Blatt und wählst für die Gewichtskragt eine Vektorlänge, die ca. 1/4 der Blattbreite beträgt (meine Schätzung). Jetzt verlängerst Du den Vektor, an dem die Last hängt über den Knotenpunkt nach oben und trägst darauf die Gewichtskraft auf. Von diesem Punkt zeichnest Du Parallelen zu beiden schrägen "Seilen", die die Spitze des zuletzt gezeichneten Vektors treffen. Jetzt mußt Du nur noch die Längen der Vektoren (=Parallelohrammseiten) in Relation zur angehängten Gewichtskraft setzen. Das sollte dann so aussehen, wie ProfFrink es in seiner Antwort beschrieben, gerechnet und gezeichnet hat.
Probiere es in jedem Fall selbst mal aus!
Hier die Antwort auf dem Silbertablett.
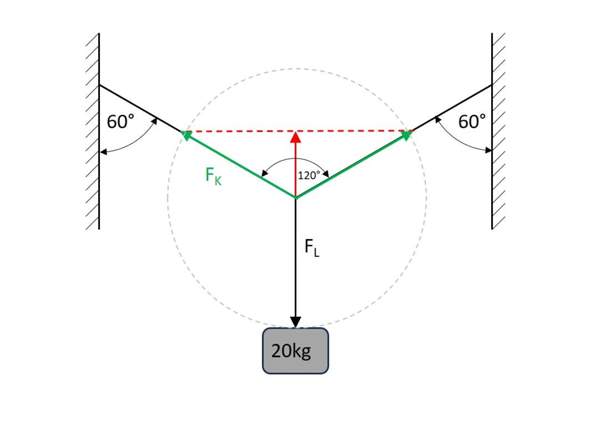
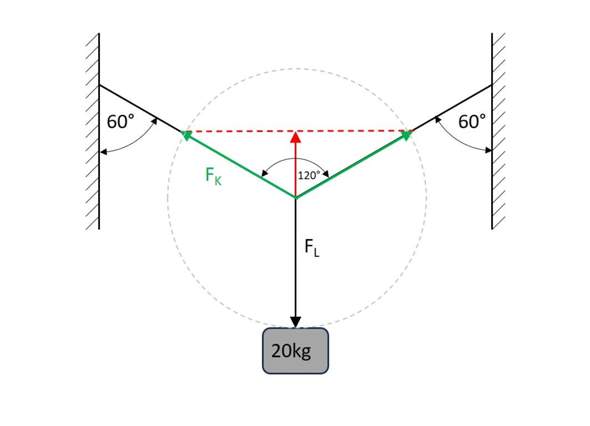
Die Summe der beiden grünen Kraftpfeile in den Kabel muss als vertikale Komponente die Gewichtskraft F_L kompensieren. Darum ist der rote Pfeile halb so lang wie der schwarze Pfeil. Die horizontalen (grüne) Kraftkomponenten müssen sich aufheben. Der Betrag des grünen Kraftpfeils kann nun zeichnerisch ermittelt werden oder kann mit der cos-Beziehung ausgedrückt werden.
Aufgelöst nach F_K erhält man
Somit erhält man das überraschende Ergebnis, dass jede Kabelhälfte die gleiche Kraft auffängt wie die Gewichtskraft selber. Der graue Kreis deutet es an.
Leider wahr. Ich brauchte heute noch eine dritte Antwort um die Tagesmission zu erfüllen. Das hat mich getrieben.
OK, das ist auch eine Möglichkeit. Ich versuche möglichst den Weg zu zeigen, bei dem noch Eigenleistung übrig bleibt. Manchmal ist der direkte Weg der Schnellere, aber das Fördern von Eigenleistung ist mir wichtiger...
Diese Antwort ist korrekt. Sie lädt leider nicht zum Selbstdenken ein, weil sie "schluckfertig eingespeichelt" ist... ;--)