Wie kann man bei dieser Aufgabe das totale Differenzial berechnen?
Hallo liebes Forum,
ich habe hier die Ableitungen nach x1 und x2 gebildet.
Jetzt komme aber nicht mehr weiter und würde gerne eure Hilfe in Anspruch nehmen. Die Formel für das totale Differenzial habe ich aufgeschrieben.
Kann mir da jemand helfen bei der Rechnung?
Danke
Marc

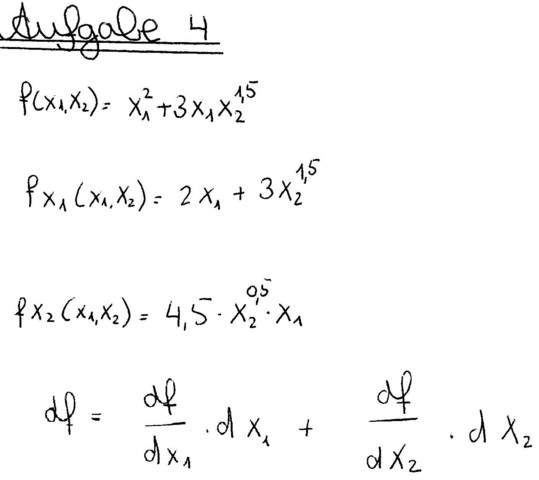
2 Antworten
Hallo,
wenn Du die beiden partiellen Ableitungen gebildet hast, multiplizierst Du die Ableitung nach x1 mit dem Unterschied zwischen 1,1 und 1, also mit 0,1
und die Ableitung nach x2 mit dem Unterschied zwischen 2 und 2,05, also mit 0,05.
Anschließend wird beides addiert.
Dieser Wert ist eine Näherung für den Wert, den Du erhältst, wenn Du den Funktionswert von (1|2) vom Funktionswert von (1,1|2,05) abziehst, spart also etwas Rechenaufwand.
Genauer ist natürlich die zweite Methode.
Konkret:
Ableitung nach x1=2x1+3*x2^(1,5)
Ableitung nach x2=4,5x1*x2^(0,5)
Die Näherungsmethode funktioniert nun so:
Du gibst den Punkt (1|2) ein, multiplizierst die Ableitung nach x1 mit 0,1, also dem Unterschied zwischen 1,1 und 1:
0,1*(2+3*2^(1,5))=1,048528137
Die Ableitung nach x2 multiplizierst Du mit 0,05, also 2,05-2.
Auch hier setzt Du den Punkt (1|2) ein:
0,05*(4,5*2^(0,5))=0,3181980515
Anschließend addierst Du die beiden Werte:
1,366726189
Das ist die Näherungslösung.
Genauer wird es, wenn Du einmal den Punkt (1,1|2,05) in die Funktion einsetzt und davon dasselbe mit Punkt (1|2) abziehst:
(1,1²+3*1,1*2,05^1,5)-(1²+3*2^1,5)=1,410724575
Näheres findest Du hier:
http://massmatics.de/merkzettel/index.php#!221:Totales_Differential
Herzliche Grüße,
Willy
Eben, beide Lösungen weichen durchaus voneinander ab.
In der Beispielaufgabe, die in dem Link durchgerechnet wird, beträgt die Abweichung 0,1. Näherung: 2,1, Wert: 2,2.
Willy
Das totale Differenzial gibt ja die Steigungen in x1 bzw x2 Richtung an. Du hast den Wert f(1,2) der Funktion an der Stelle (1,2) und möchtest jetzt den Wert der Funktion bei (1.1,2.05) haben. Du hast auch das totale Differenzial (sagen wir: (a,b)) an der Stelle (1,2). Also ist an der Stelle (1,2) eine Steigung von a in x1 und von b in x2-Richtung. Du gehst also linear in diese Richtungen und hast ungefähr:
f(1.1,2.05) = f(1,2) + (a,b)*(0.1,0.05) = f(1,2) + (0.1a, 0.05b)
Du bist im Moment echt Mathe am lernen oder? :D Oder hast du nur die Ferienhausaufgaben vergessen? Und in welcher Schule macht man so etwas?
Achso das ergibt Sinn :-) Weil du als Tag Gymnasium hast, hatte ich mich gewundert. Mehrdimensionale An*lysis ist schon was spannendes, man muss sich nur etwas an die ganzen Matrizen gewöhnen ;-) Jacobimatrizen solltest du dir auf jeden Fall mal angucken.
Hi, ich übe gerade Mathe mit einem Lernbuch. Das ist keine Schule, ich gehe schon Jahrzehnte nicht mehr in die Schule. Besuche eine Hochschule und mache dort aufgaben aus dem buch, lösungen gibt es leider keine und die erklärungen lassen wünsche offen.
Willy vielen lieben Dank. Ich habe beide Verfahren berechnet, sowohl die genaue Lösung mit den Punkten als auch die Näherungslösung, ich dachte, es muss übereinstimmen, aber da das differenzial nur eine näherung darstellt, ist das ding ja gegessen.