Wie kann ich die Nullstellen dieser E-Funktion berechnen, weil wenn ich die 1 mit -1 auf die andere Seite bringe, dann geht ja kein ln?
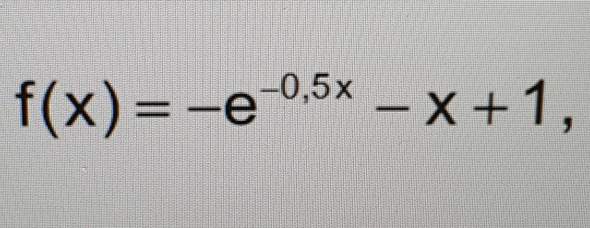
6 Antworten
Hallo,
eine triviale Lösung ist x=0.
Die andere findest Du nur durch Näherungsverfahren oder über die Lambertsche W-Funktion. x=-2,51286242 (gerundet).
Um die Lambertsche W-Funktion, die Umkehrfunktion zu y=u*e^u nutzen zu können, mußt Du die Gleichung natürlich erst einmal auf diese Form bringen.
Das geht mit Hilfe von Äquivalenzumformungen und der anschließenden Substitution
0,5x-0,5=u.
Darüberhinaus braucht es ein Programm, das den nötigen Wert ausspuckt, diese Funktion demnach beherrscht.
Alternativ wäre das Newton-Verfahren mit Startwert -2,5 zu versuchen.
Herzliche Grüße,
Willy
0=-1*e^(-0,5*x)-x+1
Mit meinem Graphikrechner (GTR,Casio) x1=-2,5128.. x2=0
Mit normalen Mitteln in Handarbeit nicht lösbar
1) eine Stelle angenähert durch probieren ermitteln und dann eine der beiden Näherungsformeln von Newton (Tangentenverfahren) oder Reguls falsi (Sehnenverfahren) anwenden
Infos per Bild,vergrößern und/oder herunterladen


Beide Seiten mit -1 multiplizieren, da ja auch ein - vor dem e steht. Das darf ja genauso wenig in die ln() Funktion, wenns negativ ist.
Bringe …
(-1) / √e^x - x
… durch Addition auf die andere Seite der Gleichung, dann hast nur positive Werte.
Was willst denn mit der 1? Die bleibt, wo sie ist.
Bei …
f(x) = (-e)^(-x/2) - x + 1 = 0
… addierst e^(-x/2) und x und bekommst …
<=> e^(-x/2) + x = 1
Alternativ „bewegst“ nur die 1 durch Subtraktion …
<=> (-e)^(-x/2) - x = (-1)
… und dividierst dann durch (-1) …
<=> e^(-x/2) + x = 1
Wer verlangt, dass du die Nullstelle berechnest?
Das lohnt sich bei solchen Aufgaben immer. Ist aber leider nicht die einzige Nullstelle.
Ich vermute, dass in der Aufgabenstellung bestimme steht -> GTR
Das kann sein. Anders ist das für Schüler kaum lösbar; es sei denn, sie üben gerade das Newton-Verfahren.
Ich fürchte, die Zeiten, wo soetwas unterrichtet wurde, sind vorbei...
Also erstens= f(x)=0
dann -x und + 1 auf die adere Seite,
dann steht ja -e^-0,5x = x -1 jetzt mal -1
aber dann wird ja mein x wieder negativ