Wie errechnetman f?

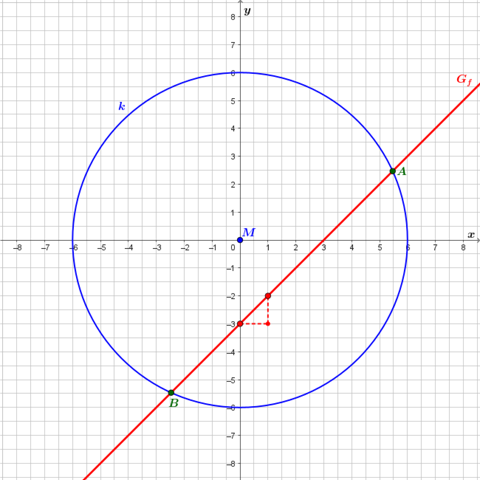
Der Kreis ( Radius 6cm ) wird durch den Graphen der linearen Funktion mit der Funktionsgleichung y= f(x) =x-3 geschnitten
Wie groß ist f?
2 Antworten
Was meinst du mit „Wie groß ist f?“? Da gibt es keine konkrete Größe, die man berechnen kann. f ist eine Funktion. Und die Funktionsgleichung y = f(x) = x - 3 hast du gegeben.
Der Graph einer lineare Funktion mit Funktionsgleichung y = m x + t ist eine Gerade mit Steigung m und y-Achsenabschnitt t. Im konkreten Fall hast du bei der Funktion f dann mit y = x - 3, was man auch als y = 1 x + (-3) darstellen kann, eine Gerade mit Steigung 1 und y-Achsenabschnitt 3 als Funktionsgraphen.
Beginne also (entsprechend dem y-Achsenabschnitt -3) auf der y-Achse beim Wert -3. [Markiere dir diesen Punkt auf der y-Achse.] Von dort aus gehe eine Einheit nach rechts und (entsprechend der Steigung 1) eine Einheit nach oben. [Markiere dir den so erreichten Punkt.] Zeichne dann eine Gerade durch die beiden Punkte.
[Alternativ könntest du auch eine Wertetabelle anlegen, und dir zu einigen x-Werten den entsprechenden y-Wert y = x - 3 berechnen. Dann wirst du merken, dass die entsprechenden Punkte (x | y) alle auf einer Geraden liegen. Zeichne die entsprechenden Punkte ein und zeichne eine Gerade durch diese Punkte.]

Ich weiß nun nicht, was du mit „Wie groß ist f?“ bzw. „Wie errechnetman f?“ meinst.
====== Ergänzung ======


Vielen Dank für deine Antwort, hat mir sehr geholfen, jetzt noch eine Frage :
Parallel zuy= f(x) verläuft durch den Koordinatenursprung eine weitere lineare Funktion y=g (x)
Zeichne g(x) ein
Gib die Funktionsgleichung für y= g(x) an
Zeichne eine Gerade parallel zur vorigen Geraden (also mit gleicher Steigung 1), welche durch den Koordinatenursprung M(0|0) verläuft (also mit y-Achsenabschnitt 0).
Ich habe mal das Bild entsprechend in meiner Antwort ergänzt.
Der Kreis vom Radius 6 lässt sich implizit beschreiben durch die Gleichung
nun gilt ja für die y-Koordinate deiner Geraden:
setze es oben in die erste Gleichung ein und du erhältst:
löse diese Gleichung nun nach x auf und du erhältst die gesuchten (zwei) x-Koordinaten, diese kannst du dann in y = x - 3 einsetzen und hast dann beide Koordinaten. Die Strecke kannst du dann selber bestimmen, oder? Sollte doch eigentlich dann der leichteste Teil sein.
Danke danke danke
Und jetzt eine letzte Frage:
Vom Koordinatenursprung senkrecht zu y=g(x) verläuft eine Strecke,die den Kreis in P schneidet.
Zeichne die Strecke PM ein
Gib die Koordinaten von P an
Zeichne in P an den Kreis eine Tangente t