Wie berechnet man hier die Fläche des Kreissegments?
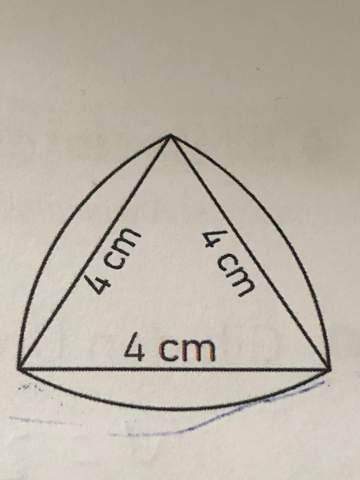
Hallo ich hab hier eine Aufgabe man soll die Fläche der Kreisegmente (gelb markiert) berechnen Angabe: es ist ein gleichseitiges Dreieck alle Seiten haben 4cm und der Radius der Kreissektoren ist auch 4cm aber Ich komm nicht auf das richtige Ergebniss mein Rechenweg:
Asektor= (60:360)•4cm2•pi. Asektor=8,38cm2 (hier soll eigentlich 4,35cm2 rauskommen)
Adreieck= (4cm2:4)• Wurzel aus 3 Adreieck=6,93cm2
Agelb=3•8,36-6,93
Agelb=18,15 (hier soll 11,27cm2 rauskommen)
was mache ich falsch?
5 Antworten
Hallo,
die Gesamtfläche bekommst du, indem du drei Kreissektoren, die zusammen einem Halbkreis entsprechen, nimmst und zweimal die Fläche des Dreiecks subtrahierst.
A=0.5π•4² - 2• 4²/4 •√3=11.276
🤓
In dem Sektor ist das Dreieck enthalten. Du subtrahierst bei A_gelb aber nur einmal das Dreieck, statt zweimal.
A_gelb = 3 * 8,36 - 2 * 6,93 = 11,22 (passt, bis auf Rundungsdifferenzen)
A_Sektor = r² * π * 60° / 360° = 8,378 cm²
A_Dreieck = (√(3) / 4) * a² = 6,928 cm²
A_Kreisabschnitt = A_Sektor - A_Dreieck = 1,450 cm²
A_ges_ = 3 * A_Kreisabschnitt + A_Dreieck = 11,28 cm²
ich denke die Lösung ist falsch
so müsste es sein
( pi*4²*1/6 - 3^0.5* 4²/4 ) * 3 ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, in der Klammer steht die Fläche eines Segments.
.
und hier fehlt m.E eine Klammer
Agelb = 3 • (8,36-6,93) ...............ohne Klammer rechnest du 3 Sektoren minus 1 Dreieck
was ist denn nun gelb markiert , wir und du auch , sehen nix . Diese drei Teile ?
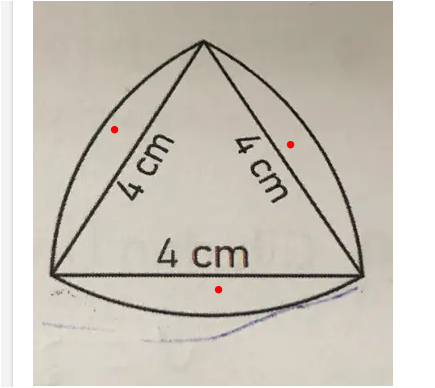
für die drei Teile stimmt meine Lösung
11.27 ist die Fläche des ganzen , was man sehen kann.
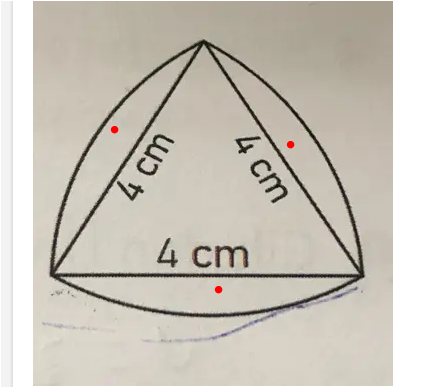
Fläche Kreissegment = Teilkreisfläche - Dreiecksfläche
Teilkreisfläche = 60°/360° * pi * 4² = 8,38 cm²
Dreiecksfläche = Wurzel(3) / 4 * a² = 6,92 cm²
Fläche Kreissegment = 8,38 - 6,92 = 1,45 cm²
Alle 3 Kreissegmente zusammen: 3 * 1,45 cm² = 4,35cm²
3 Kreissegmente + 1 Dreieck = 4,35 cm² + 6,92 cm² = 11,27 cm²
Bei dir ist nichts farblich markiert.
Fläche des Gesamtkreises = Pi mal r^2
Geteilt durch 6 (alle Winkel in einem gleichseitigen Dreieck = 60°).
Minus Fläche des Dreiecks - kommt die Fläche für ein Kreissegment raus.
Das mal 3 = Fläche aller 3 Segmente zusammen!