Wie berechnet man die Dachfläche mithilfe des Satz des pythagoras?
7 Antworten
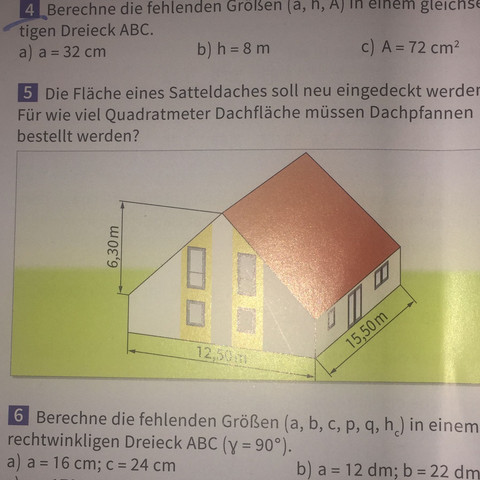
Du brauchst die Länge der schrägen Seiten des Daches. Zeichne nur den oberen Dachteil des Hauses von der Forderseite. Du hast ein Dreieck. Die linke und die rechte Seite sind gleich lang. Die untere Seite ist 12,50. Jetzt kann du durch die Mitte eine Linie ziehen (sie ist 6,30m) und hast 2 rechtwinklige Dreiecke. In denen darfst du dann Pythagoras benutzen. Deine beiden rechtwinkligen Dreiecke sollten die Seiten 6,30m und 6,25m haben, dann hast du alles richtig gemacht. Die Hypothenuse ist die Seite die du suchst, weil sie dem rechten Winkel gegenüberliegt. Diese Seite kannst du jetzt mit Pythagoras berechnen. Das Dach besteht aus 2 Rechtecken, wie du bei Brainchild schön sehen kannst. Die Seite wo bei ihm 6,30m steht ist allerdings in Wirklichkeit das was du gerade ausgerechnet hast.
Die schräge Dachseite d ist die Hypotenuse eines rechtwinkligen Dreiecks mit den Katheten
h = 6,30 m und g = Giebelseite / 2 = 6,25 m
Darauf wendest den Satz des Pythagoras an und erhältst
d² = h² + g²
Mit l = 15,5 m berechnest dann die gesamte Dachfläche
F = 2 • d • l
Für die Dachfläche braucht man keinen Phytagoras. Das sind 2 Rechtecke:




Hast ja recht, die 6,3m sind paralell zur Wand und nicht zum Dach.-)
Berechne die Dachschrägenlänge aus den Katheten Höhe des Daches und halbe Hausbreite.
15,50 × 6,30 × 2
Dir fehlen dann 79,80 m² Dachfläche, also plane mehr Fenster mit ein.
Die 6,30 sollen die Höhe des Daches sein. Im rechten Winkel zum Erdboden. Du hast also die Seitenlänge der einen Seite nicht und musst genau diese durch Pythagoras errechnen.