Wer kann mir dabei helfen?Matheproblem?

Answer 1

[mihisu]

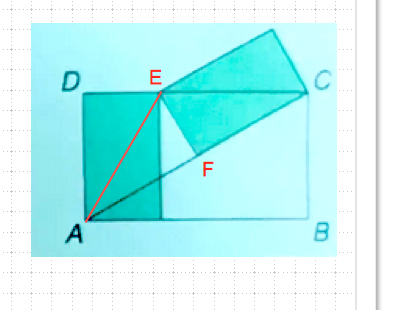
Ich habe mal einige zusätzliche Punkte benannt, damit klarer ist, was ich im Folgenden meine.

Die Dreiecke AIH und HGF sind kongruent zueinander, denn...

• Die Winkel ∠AHI und ∠GHF sind gleich groß (Scheitelwinkel).
• Die Winkel ∠HIA und ∠FGH sind gleich groß (nämlich beide 90°, da die grauen Vierecke Rechtecke sind).
• Damit sind dann auch die Winkel ∠IAH und ∠HFG gleich groß (wegen Innenwinkelsumme in den Dreiecken AIH bzw. HGF).
• Außerdem sind die Strecken [AI] und [FG] gleich lang.
• Wegen WSW-Kongruenzsatz folgt dann, dass die Dreiecke AIH und HGF kongruent zueinander sind.

Da diese beiden Dreiecke kongruent zueinander sind, haben sie insbesondere den gleichen Flächeninhalt, welchen ich im Folgenden mit A₂ bezeichne.

Die beiden Dreiecke FGC und CEF sind offensichtlich wegen SWS-Kongruenzsatz kongruent zueinander. Die beiden Dreiecke FGC und CEF haben also den gleichen Flächeninhalt, welchen ich im Folgenden mit A₃ bezeichne.

Für den Flächeninhalt der (ursprünglich grauen) Rechtecke AIFD und FGCE, der andererseits auch 3 cm² betragen soll, erhält man nun...

$A_1+A_2=3\,\text{cm}^2$

$2\cdot A_3=3\,\text{cm}^2$

Außerdem setzt sich die obere-linke Hälfte der Fläche des Rechtecks ABCD aus A₁ + A₂ + A₃ zusammen. Der gesuchte gesamte Flächeninhalt des Rechtecks ABCD ist dann das doppelte dieser Hälfte also...

$2\cdot \left(A_1+A_2+A_3\right)$

$=2\cdot \left(A_1+A_2\right)+2\cdot A_3$

$=2\cdot 3\,\text{cm}^2+3\,\text{cm}^2$

$=6\,\text{cm}^2+3\,\text{cm}^2$

$=9\,\text{cm}^2$

Dementsprechend ist Antwortmöglichkeit (B) richtig.

Comments

[Alexa197]

Hey vielen Dank auch

Answer 2

[Hamburger02]

B) 9 cm^2

∆EFC = 1,5 cm^2

∆AFE = ∆EFC = 1,5 cm^2

∆AED = ∆AFE = ∆EFC = 1,5 cm^2

∆ACD = 3 * 1,5 cm^2 = 4,5 cm^2

☐ABCD = 2 * ∆ACE = 9 cm^2

Comments

[Alexa197]

Hey vielen Dank!!!!

[Randomguy990]

@Alexa197

Welche Klasse Känguru ist das?

[Alexa197]

@Randomguy990

9.

[Alexa197]

Wie kommst du darauf?

[Hamburger02]

@Alexa197

siehe oben

Answer 3

[SevenOfNein]

Wie lange ist die Strecke A-B.

Und wie breit das graue Rechteck, das grün ist 🖖

Comments

[Alexa197]

nicht bekannt

[SevenOfNein]

@Alexa197

Miss mal nach auf dem Bild

[Alexa197]

@SevenOfNein

Ist nur ne Skizze

[SevenOfNein]

@Alexa197

Egal, sag an.

[mihisu]

@SevenOfNein

Die Länge der Strecke [AB] beträgt (432)^(3/4)/24 cm, also etwa 3,948 cm.

Je nachdem, welche der beiden Seitenlängen der grauen Rechtecke du als „Breite“ ansiehst, beträgt die Breite eines grauen Rechtecks (432)^(3/4)/72 cm oder (432)^(1/4)/2 cm, also etwa 1,316 cm bzw. etwa 2,280 cm.

Das ist aber für die Lösung der Aufgabe gar nicht so relevant. Die Aufgabe (ohne Berechnung dieser Längen) zu lösen ist deutlich einfacher als die Berechnung dieser Längen.

Und: Je nach dem, wie das vielleicht beim Drucken gestreckt bzw. verzerrt worden ist, hilft es auch nichts die Längen im Bild zu messen. [Wenn die Zeichnung überhaupt maßstabsgetreu ist, nicht nur eine Skizze.]