Wenn Ableiten das Messen der Steigung ist, weshalb ist das Gegenteil das Integrieren?
Warum ist das Gegenteil zur Steitung, die Flächenvermessung?
8 Antworten
Die Frage ist in der Tat sehr gut. Es handelt sich zwar ganz klar um einen einigermaßen leicht beweisbaren mathematischen Zusammenhang, nämlich um den "Hauptsatz der Differential- und Integralrechnung", das hast du aber auch gar nicht infrage gestellt. Vielmehr würde ich die "warum" Frage so verstehen, dass du eine anschauliche Erklärung möchtest, alternativ fragst du nach dem tieferen, philosophischen Sinn aber einmal gibt es etwas in der Art bei einem mathematischen Ausdruck nicht und ich denke, darauf wolltest du auch nicht hinaus.
Also wie gesagt: Formal und mathematisch kann man diesen Umstand beweisen, das gibt aber nicht unbedingt direkt Einsicht, warum die Fläche unter der Kurve der Steigungsfunktion nun unbedingt du ursprüngliche Funktion reproduzieren muss, also (etwas illustrativ):
f(x) = Fläche(Steigung(f(x)))
Der Korrekte Term wäre wohl "Umkehrung", nicht "Gegenteil" aber darauf haben andere genügend rumgehackt ;).
Zur Erklärung: Die Fläche unter einer Kurve kann man (etwas abhängig von der verwendeten Definition für das Integral) als die Summe vieler (infinitesimal) kleiner Rechtecke unter der Kurve ansehen. Die Ableitung ist wiederum die Steigung der Funktion (bzw. einer Sekanten) zwischen zwei (infinitesimal) nahen Punkten auf einer Kurve.
Betrachten wir also einen sehr kleinen Abschnitt einer beliebigen Kurve. Dieser (infinitesimal) kleine Abschnitt wird näherungsweise wie eine Gerade verlaufen (solange es sich um eine stetige Funktion handelt aber andernfalls wäre die Funktion an der Stelle auch gar nicht differnzierbar). Ich hoffe es erscheint anschaulich klar, dass wenn diese zwei Punkte auf der Kurve sehr nahe bei einander liegen, die Steigung der Sekanten der Steigung der Tangente zwischen den beiden Punkten immer ähnlicher wird, sobald der Abstand der Punkte Null beträgt ist beides identisch (das ist auch die gebräuchliche Definition der Ableitung), gleiches gilt für die Fläche und das Integrieren. Folglich sollte anschaulich klar sein, dass eine lokale Erklärung des Zusammenhangs an einer (lokal) linearen Funktion den allgemeinen Zusammenhang erklärt (falls nicht werde ich das gerne noch weiter ausführen ;D).
Die Fläche unter einer Geraden ist gegeben durch:
Fläche(f(x)) = df*dx/2+b*dx = m*dx²/2 + b*dx
Anmerkung: Das war keine Integration, vielmehr habe ich die Fläche Dreiecks unter der Kurve (df*dx/2) und die des durch den y-Abschnitt ergebenden Rechtecks addiert (das Ergebnis ist das aber natürlich identisch mit dem der Integration).
Die Steigung der sich ergebenden Parabel kann man nun über die Ableitung bestimmen oder mit einer beliebigen anderen Methode, was man erhält ist:
Steigung(Fläche(f(x))) = m*dx + b
Nun ist mir klar, dass es sich dabei nur um einen relativ anschaulichen Beweis für den Hauptsatz handelt (vielleicht genügt dir das ja bereits, da du nun ein illustratives Bild der Methode hast), die Tatsache, dass es so ist, bleibt natürlich dennoch erstaunlich und damit eines der "Wunder" der Mathematik ;)
Addition - Subtraktion
Multiplikation - Division
Potenzierung - (Radizieren, Logarithmieren)
sin - arc sin (und auch alle anderen Winkelfunktionen)
Differentiation - Integration
Alle kannst du gegeneinander aufheben,
das ist also beim Ab- und "Aufleiten" gar nichts Besonderes.
Man nennt das Prinzip bei diesen beiden
"Hauptsatz der Differential- und Integralrechnung".
https://de.wikipedia.org/wiki/Fundamentalsatz_der_Analysis
Es hat natürlich zur Folge, dass beispielweise auch die meist so genannte Originalfunktion die Ableitung eines Integrals ist oder die 1. Ableitung das Integral der zweiten.
Das kannst du probieren und verifizieren.
Nimm z.B. die Abfolge:
x³/3 .......... x² ........... 2x ................. 2
Nach rechts hin wird abgeleitet, nach links hin wird integriert (hier mal ohne C wegen der Übersichtlichkeit).
Ich würde nicht vom Gegenteil sprechen. Sondern es ist etwas ähnliches wie die Umkehrfunktion bzw. die Umkehrung der Fragestellung bzw. der fast logische Umkehrschluss aus einer (mathematisch formulierbaren) Aussage.
Kurz (als Umkehrfunktionen verstanden):
Ableitung/Steigung ist eine Division (z.B. Aenderung pro Zeit, geometrisch eine Steigung),
Integral/Fläche ist eine Multiplikation (Grösse mal Zeit = geometrisch eine Fläche).
Beispiel: In der Praxis wird ja oft ja nach der Zeit abgeleitet bzw. über die Zeit integriert, damit ist es auch am anschaulichsten erklärbar. Hier der Einfachheit halber mit abschnittweise konstanten Werten):
- Wenn etwas in gleichen Zeitabschnitten um gleich viel ändert (Steigung), dann gilt das als konstante Aenderung. Hier drin steckt eine Division: Aenderung der Grösse pro Zeitabschnitt => Die Ableitung dieses Zeitverhaltens sagt: die Aenderungsrate hat einen konstanten, bestimmten Wert.
- Umkehraussage: Wenn der Verlauf einer Aenderungsrate zeitlich bekannt und konstant ist, so kann man daraus die aktuelle Grösse ermitteln, indem man sie mit der vergangenen Zeit multipliziert. So entsteht dann die Fläche unter der Kurve => Das Integral dieser Aenderungsratenfunktion über die Zeit sagt, dass die ändernde Grösse selbst eben eine konstante Zu- oder Abnahme (Steigung) hat.

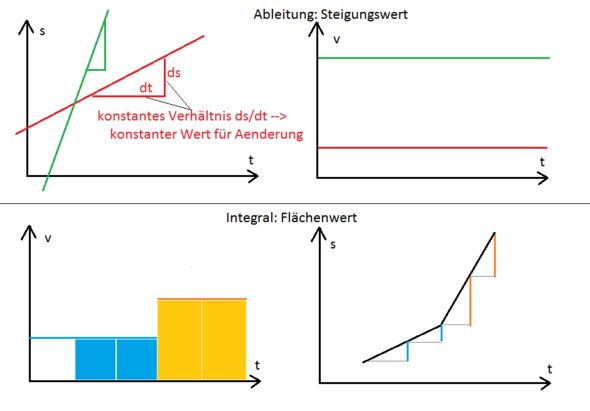
Das Wort "Gegenteil" ist hier sehr unschön. Vielleicht mal ein Beispiel: Was ist das Gegenteil von gehen. Mhh, vielleicht rückwärts gehen oder sich hinsetzten oder gar nicht tun oder... Ein Gegenteil gibt es also nicht.
Beim Integrieren versucht man mathematisch das Differenzieren (Ableiten) umzukehren. Im Prinzip ist das Verhältnis der beiden Begriffe wie "vorwärts laufen" und "rückwärts laufen". Das eine ist nur der umgekehrt Vorgang vom anderen.
Rückwärts fahren ist nicht das Gegenteil von vorwärts fahren.
Genauso ist Integration nicht das Gegenteil der Differenzierung, sondern beides sind Anwendungen auf Funktionen, nur in unterschiedliche Richtungen.