Was bedeutet das in der Stochastik?
Ich will Mathe nachholen für mein Abitur im Oktober diesen Jahres und mache gerade Stochastik, lerne mit dem Abiturbuch von Daniel Jung und wollte fragen, ob mir das mal jemand erklären kann, was in dem grauen Kasten steht, also was als Eigenschaften deklariert ist.

Eigentlich hatte ich bis zum Fachabitur nie Probleme mit Stochastik, war immer ein Mathe 1 Schüler, doch als ich ins Fachabitur kam und das 1 Jahr übersprungen habe und so im zweiten und letzten Jahr des Fachabiturs war, war alles anders, habe aber auch nie Unterricht genacht sondern nur blödsinn.
Bis dahin hatten wir immer mit dem "Baum" in Stochastik gearbeitet und plötzlich haben wir diese Mathezeichen A,B/[,],(,) usw. Klasse wae auf zwei geteilt (wegen Covid) und die Lehrkraft war überwiegend nur in der anderen Hälfte. 45 Minuten eine Unterrichtseinheit und er war nur so 15 Min. bei uns, achja und wir waren nicht die gute Hälfte, sondern die "miese". Und wenn er da war, lag er damit los und hüpfte direkt von den Punkt dahin und dann dahin. Hab mal in die Paralelklasse geguckt und die Lehrkraft dort nahm sich Zeit und war nicht so ne die Frage stell mir privat keine Zeit zur Antwort.
Danke im Voraus.
Ps: Falls wichtig, werde Biologie studieren.
3 Antworten
1)
Der Ausdruck

meint nichts weiter, als dass die Wahrscheinlichkeit eines Ereignissen A mindestens Null, maximal Eins oder irgendwo dazwischen ist. Z.B. P(A)=½.
Es gibt also keine Wahrscheinlichkeit, die größer als Eins bzw. kleiner als Null ist.
2)
Die Ausdrücke

meinen, dass die Wahrscheinlichkeit für irgendein mögliches Ereignis, also die "Grundmenge" des Wahrscheinlichkeitsraums, - das sichere Ereignis - die höchst mögliche Wahrscheinlichkeit (nämlich Eins) zugeordnet ist und die Wahrscheinlichkeit für kein mögliches Ereignis, also die leere Menge, - das unmögliche Ereignis - die kleinst mögliche Wahrscheinlichkeit (nämlich Null) zugeordnet ist.
3)
Der Ausdruck

meint nichts weiter, als dass die Vereinigung zweier möglichen Ereignisse die selbe Wahrscheinlichkeit haben wie die Summe der Wahrscheinlickeiten der einzelnen Ereignisse. Wenn A und B nicht disjunkt sind, also beide mindestens ein selbes Element besitzen, muss man die Wahrscheinlichkeit der Schnittmenge noch abziehen.
4)
Der letzte Ausdruck

meint nur, dass für die Wahrscheinlichkeit des Gegenereignisses auch die Gegenwahrscheinlichkeit zählt. Das Gegenereignis ist das Ereignis von A, wo alle Elemente der Grundmenge außer die aus A vorhanden sind.
Ich hoffe, ich konnte helfen :)
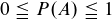
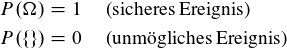
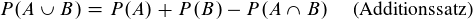
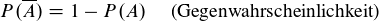
Ja... finde die andere Antwort eigentlich sogar besser. Vergess dieser nicht die Auszeichnung "Hilfreichste Antwort" zu verleihen, sobald es möglich ist ;)
(1): P(A) ist die Wahrscheinlichkeit, dass Ereignis A eintritt. Diese bewegt sich immer zwischen 0 und 1 (mit 0 und 1 eingeschlossen), also von 0% bis 100%.
(2): P(Ω) ist die Wahrscheinlichkeit, den Ergebnisraum zu treffen. Der Ergebnisraum ist dabei einfach die Menge aller möglichen Ergebnisse.
Beim Würfel ist Ω = {1, 2, 3, 4, 5, 6}. Die Wahrscheinlichkeit eine dieser Zahlen zu treffen ist logischerweise immer 1 oder 100%.
P({}) ist quasi die Wkt. kein mögliches Ergebnis zu treffen, was aber immer 0 sein muss, da irgendein Ergebnis eintritt. Wird auch als "unmögliches Ereignis" bezeichnet.
(3): A u B ist die Vereinigung der Mengen A und B. Beim Würfel könnte A = {1, 4} sein, also das Ereignis, dass eine 1 oder 4 gewürfelt wird. Und B = {1, 5} analog.
Wenn du nun P(A u B) mit A u B = {1, 4, 5} berechnen willst, kannst du einfach die Einzelwahrscheinlichkeiten addieren und die Wkt. für den Durchschnitt abziehen.
P({1, 4, 5}) = P({1, 4}) + P({1, 5}) - P({1}) = 1/3 + 1/3 - 1/6 = 3/6 = 1/2.
(4): Das Gegenereignis (A mit Strich drüber) ist quasi "alles außer A".
Wenn beim Würfel A = {2, 6}, dann ist Nicht-A = {1, 3, 4, 5}.
P(Nicht-A) = 1 - P(A) = P(Ω) - P(A) = P({1, 2, 3, 4, 5, 6}) - P({2, 6}) = P({1, 3, 4, 5})
Super, vielen dank, logisch und unkompliziert erklärt, danke.
warum Herr Jung das so schreibt oder in Kapiteln vor 1.4 dieses erwähnt :
Die Axiome von Herrn Kolmogorow sind es , auf die es ankommt
Deine und die andere Antwort haben mir echt weiter geholfen, vielen Dank.