Wächst eine Logarithmus Funktion langsamer als ALLE Wurzelfunktionen?
Mir ist bewusst das die Antwort auf die Frage "Ja" lauter allerdings würde ich gerne wissen wie man das ganze beweisen bzw zeigen kann. Hoffe ihr könnt mir dabei weiter helfen.
3 Antworten
Es ginge also darum, zu beweisen, dass
limes (x -> ∞) [log_a(x) / x^(1/n)] = 0
für alle a mit a > 1 (!) und für alle natürlichen Zahlen n .
Wegen log_a(x) = ln(x) / ln(a) und weil a als konstant betrachtet werden soll, kann man auf den konstanten (positiven) Nenner ln(a) verzichten und zeigen, dass
limes (x -> ∞) [ln(x) / x^(1/n)] = 0
für alle natürlichen Zahlen n .
Nun kann man den Satz von l'Hospital benutzen (warum ?), um den Grenzwert zu ermitteln.
Ich habe vorausgesetzt, dass die Logarithmusbasis größer als 1 sein soll (wie man das allermeistens auch hält). Allerdings würde das Ganze auch für eine Basis a mit 0 < a < 1 gehen.
Die Aussage ist falsch. Es müsste gelten
ln(x) < x^(1/n) für x -> ∞ und alle natürlichen Zahlen n, also
e^( ln(x) ) < e^(x^(1/n))
x < e^(x/n)
Nun kann man immer eine natürliche Zahl n finden mit n >= x, sodass
x < e
gelten müsste. Für x -> ∞ ist das aber nicht der Fall.
Hallo surbahar53
Die Umformung von e^( ln(x) ) < e^(x^(1/n))
zu x < e^(x/n)
ist falsch, ganz einfach, weil x^(1/n) nicht dasselbe ist wie (x/n) !
So müsst's stimmen.
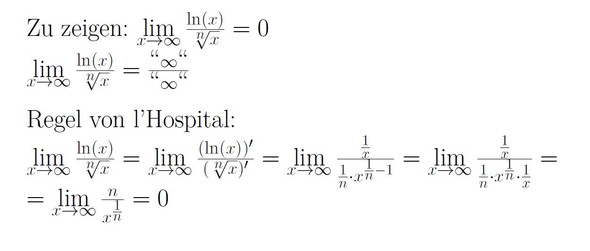
Genau.
Die Begründung, dass die Logarithmusbasis im Prinzip einerlei ist, sollte noch "mitgeliefert" werden !