Liege ich richtig, dass jede Exponentialfunktion jede andere Potenzfunktion irgendwann "überholt"?
Ich kann's grad nicht beweisen, aber einfache Beispiele zeigen es:
Exponentialfunktionen "überholen" Potenzfunktionen in ihrem y-Wert bei zunehmendem x.
Gut sichtbar ist es noch hier:
2^x überholt x^2 relativ bald.
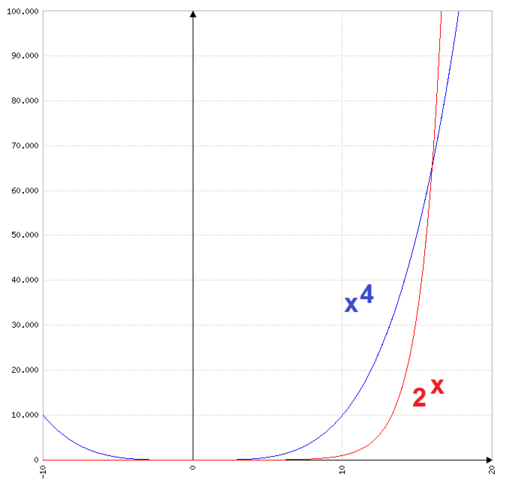
2^x überholt auch x^4, (aber erst oberhalb ca. 15, wo der Funktionswert schon ca. 65'000 ist)
Aber schwierig wird's bei 2^x > x^2000.
Wo überholt 2^x die andere Funktion? Analytische Lösung sehe ich auch grad nicht.
6 Antworten
Der Schnittpunkt der Kurven f(x)=a^x und g(x)=x^b liegt bei x=-b/ln(a)*W(-ln(a)/b), wobei W(x) die Lambertsche W-Funktion bezeichnet. Um das zu sehen, manipulieren wir die Gleichung a^x=x^b mit folgenden Schritten.
e^(x*ln(a))=x^b
e^(x*ln(a)/b)=x |setze -ln(a)/b=:t
e^(-x*t)=x
x*e^(x*t)=1 |setze x*t=:u
u/t*e^u=1
u*e^u=t (hier kommt die W-Funktion ins Spiel)
W(t)=u=x*t
x=W(t)/t q.e.d.
Da wir bereits wissen, dass die Exponentialfunktion schneller wächst als die Potenzfunktion, ist ab diesem Punkt die gewünschte Ungleichung erfüllt.
Nein, z.b. f(0)=unendlich
Untersuche e^x/x^n. L'Hospital hilft
Nein, nicht jede Exponentialfunktion überholt jede Potenzfunktion langfristig (für x gegen unendlich).
Beispiel Exponentialfunktion: f(x) = 0,1^x
Beispiel Potenzfunktion: f(x) = x²
"dass jede Exponentialfunktion jede andere Potenzfunktion irgendwann "überholt"?"
Du solltest die Aussage etwas einschränken: das gilt nämlich nur dann, wenn man eine Exponentialfunktion mit einer Basis a mit a>1 nimmt.