Unteruchen Sie die Funktionen f(x) auf Polstellen, hebbare Lücken und Asymptoten. c) f(x)= (3x-6)/(x2+2)?

30.01.2025, 10:14

Wie kann ich das berechnen?

Danke im Vorraus
teehouse  30.01.2025, 10:13

Und was ist jetzt dir Frage?

Anonym0392 
Beitragsersteller
 30.01.2025, 10:14

Sorry, vergessen reinzuschreiben. Ich weiß nicht wie man das berechnet mit der Asymptote und hebbare Lücke/Polstelle

2 Antworten

tunik123
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
rechnen, Funktion, Gleichungen
30.01.2025, 10:24

Wenn der Nenner x² + 2 ist, kann er nicht 0 werden. Also gibt es keine Polstellen oder Lücken.

Asymptote ist die x-Achse, denn wenn x gegen -Unendlich oder +Unendlich strebt, konvergiert der Funktionswert jeweils gegen 0.
Anonym0392 
Beitragsersteller
 30.01.2025, 10:28

Danke, kann man dass anhand der Polynomdivioson berechnen?

tunik123  30.01.2025, 10:33
@Anonym0392

Ich weiß nicht, wie Polynomdivision hier helfen kann.

Wenn x (positiv oder negativ) unendlich wird, kann man die 6 im Zähler und die 2 im Nenner vernachlässigen. Dann hat man 3x/x² = 3/x. Das geht gegen 0.

Wenn man die Hospitalsche Regel kennt, weiß man, dass der Grenzwert 3/(2x) ist. das geht auch gegen 0.

Ich selbst habe gleich gesehen, dass das x² im Nenner gegen das x im Zähler "gewinnt". Bloß als Lösung kann man das nicht so hinschreiben.

tunik123  30.01.2025, 10:53
@tunik123

Ich habe mich hier mal mit Polynomdivision abgequält:

(3x - 6) / (x² + 2) = 3/x - 6/x² - 6/x³ ...
 3x + 6/x
---------
 -6 - 6/x
 -6 - 12/x²
-------------
 -6/x + 12/x²

Dann habe ich die Lust verloren.

Also richtig hilfreich ist das nicht.
teehouse
30.01.2025, 10:16

Ein Hinweis: Lücken gibt es immer da, wo potentiell ungültige Rechenoperationen auftauchen:

Hier darf der Nenner natürlich nicht 0 werden. Für welche x-Werte wird er hier 0? Wenn du das hast, kannst du weitermachen.

EDIT: Und hier als Hinweis eine Funktion mit einer Polstelle bei x=2:

Bild zum Beitrag

Woher ich das weiß:Hobby – Händchen und Leidenschaft für Mathematik und Musik
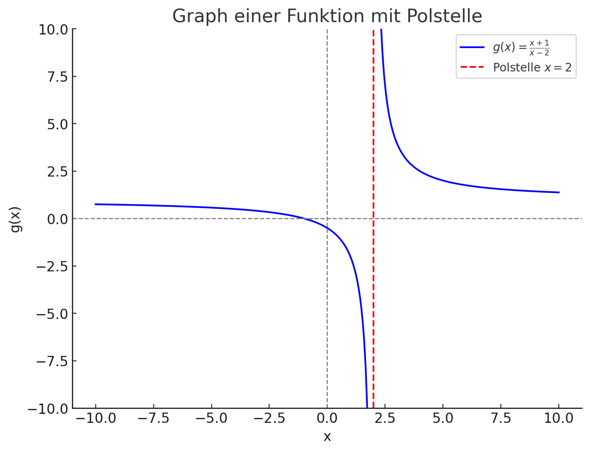
- (rechnen, Funktion, Gleichungen)
Anonym0392 
Beitragsersteller
 30.01.2025, 10:18

Der Nenner kann bei der Funktion doch aber nicht 0 werden, weil wenn man die Zahl quadriert kommt man trz immer auf eine positive Zahl, die dann plus 2 kommt man immer größer null raus

teehouse  30.01.2025, 10:20
@Anonym0392

Dann ist die Funktionsgleichung entweder falsch hingeschrieben oder es gibt tatsächlich keine Möglichkeit, dass der Nenner 0 wird. Also wohl keine Lücke und auch keine Polstelle. Wie sieht es mit der Asymptote aus?

Anonym0392 
Beitragsersteller
 30.01.2025, 10:23
@teehouse

Ja, dass verstehe ich, aber für die Asymptote muss ich die Polynomdivison anwenden, und da komme ich gerade nicht weiter

teehouse  30.01.2025, 10:25
@Anonym0392

Vielleicht hilft auch folgende Überlegung, die ich selber gerade nicht parat hatte und nachlesen musste: Du hast im Zähler und im Nenner ein Polynom. Das Polynom im Nenner hat einen höheren Grad als das im Nenner. Damit wird für hohe x in positiver und negativer Richtung der Funktionsgraph gegen y=0 laufen.