Umladevorgänge Kondensatoren (Geschmichte Schaltung von C)?
Servus zusammen :D ,
Aufgabe aus Gert Hagmann - Grundlagen der Elektrotechnik (17. Auflage)
https://i.gyazo.com/753adb32d7d109397c3e45797b392761.png
Kann mir jemand erklären, warum im Zustand S = zu die Kondensatoren C1 und C2 parallel zu C3 geschalten werden?
Mir ist klar , dass der Kondensator C3 seine Ladung abgibt und an C1 und C2 abhängig von deren Kapazität und Spannung abgibt , da Q=CU gilt.
Wäre echt nett, wenn mir jemand den Vorgang erlären könnte.
Grüße
4 Antworten
Die Kondensatoren sind vorher geladen mit
Q2=C2*U2
Q3=C3*U3
W1=Q1*U1/2
W2=Q2*U2/2
W3=Q3*U3/2
Wges = W1+W2+W3
Nach dem Entladevorgang ist
U3'=0 und daher Q3'=0
und
Q1'-Q2' = Q1-Q2
Daraus folgt
Q1'=(Q1-Q2)*C1/(C1+C2), U1'=Q1'/C1
Q2'=-(Q1-Q2)*C2/C1+C2), U2'=Q2'/C2
Man kann sich nun die Energie der drei Kondensatoren nachher ausrechnen
Wges'=W1'+W2'+W3' = Q1'*U1'/2 + Q2'*U2'/2
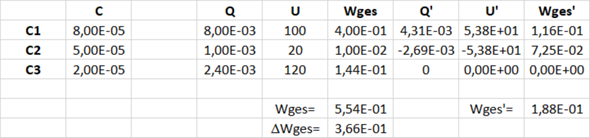
Die konkreten Werte sind:
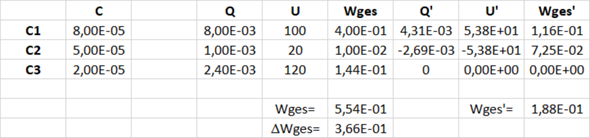
Es wird also im Widerstand die Energie von 0,366J umgesetzt.
Ich bin meit der Verwendung des Begriffs "Parallelschaltung" von C1 und C2 in der Musterlösung nicht sehr glücklich. Es ist nämlich eine Serienschaltung...
Der eigentliche Punkt ist, dass die Differenz der Ladungen in C1 und C2 konstant bleiben muss und daher die Bedingung
Q1'-Q2' = Q1-Q2
besteht. Und genau auf diesen Wichtigen Punkt wird nicht eingegangen - er fällt in der Beschreibung der Lösung vom Himmel.
Warum ist das so?
Wenn ich C1 eine Ladungmenge ΔQ entnehme, dann trifft dies auch auf C2 zu - sie liegen ja in Serie. Die Differenz bleibt daher gleich!
Mit dieser Bedingung kommt man auf die Lösung, wie ich es oben genau gezeigt habe: ΔQ ist genau so groß, bis die Gesamtspannung an C1 und C2 Null ergibt.
Die Ladungsdifferenz zwischen C1 und C2 entsteht aber nur durch den Kurzschluss über R oder ?
Davor haben C1-C3 die selbe Ladung da alle in Serie liegen ?
grüße und danke für die Geduld👍🏻
Nein, vorher ist Q1=8mC, Q2=1mC, Q3=2.4mC.
Nachher ist Q3'=0 und
Q1'=4.31mC
Q2'=-2.69mC.
Die Differenz von Q1 und Q2 ist in beiden Fällen 7mC.
Ich dachte in Serie gilt dass alle Ladungen gleich sind
Nein:
Du kannst ja (lassen wir C3 mal weg) getrennt
- C1=80uF auf 100V aufladen, ergibt Q1=8mC
- C1=50uF auf 20V aufladen, ergibt Q1=1mC
Niemand hindert dich nun, C1 und C2 in Serie zusammenzuschalten. Da weder aus C1 noch aus C2 Ladungen hinein oder hinaus können, bleibt Q1 und Q2 unverändert.
Nur wenn C1 und C2 schon gemeinsam in Serie aufgeladen werden, dann wäre Q1 und Q2 gleich. Wie der Anfangszustand erreicht wird, ist hier aber nicht wichtig.
Das gibt natürlich Sinn.
Wir hatten aufgeschrieben das es immer gilt , das war wohl mit abgelegter Spannungsquelle gemeint .
mit so Dingen wie "gilt immer..." muss man halt vorsichtig sein:
https://www.electronics-tutorials.ws/de/kondensatoren/kondensatoren-in-serienschaltung.html
https://www.elektronik-kompendium.de/sites/slt/1006081.htm
...
Für Q1‘ hast du doch (7mC*80uF)/150uF eingegeben ?
Also ich komm da auf 3.73mC.
passt aber nicht so ganz mit deiner excel.
>Für Q1‘ hast du doch (7mC*80uF)/150uF eingegeben ?
Nein ;-) das hab ich nie behauptet:
Q1'=(Q1-Q2)*C1/(C1+C2) = 7mC*80uF/(80uF+50uF) = 4,31mC
Ok , da hab ich mich wohl mehrmals vertippt haha.
ich danke dir vielmals für deine ausführlichen Erklärungen. ich rechne das jetzt nochmal auf deinem Weg 👍🏻
für mich ist die Frage dann damit vollständig beantwortet 😉
C1 und C2 sind nur eine Reihenschaltungen.
Dafür könnte auch C4 stehen. C4 hat eine Gesamtkapazitätist kleiner als C1 oder C2.
Dieser C4 ist dann mit C3 parallel geschaltet.
Zwischen den Kondensatoren gibt es so auch keine Ausgleichsströme.
Ob da der Schalter offen oder geschlossen ist.
Ja das ist mir klar.
Um die Energie auszurechnen die C1 und C2 aufgenommen haben, muss ich ja die Spannung an der Parallelschaltung errechnen. Eben C4 in deinem Beispiel. Das Funktioniert aber nur in dem ich sage U12= (Q1-Q2)/(C1+C2) wieso gilt die Formel mit einem - zwischen den Ladungen? Und nicht Q1/C1 + Q2/C2 = Q4/C4
Da die Formel für Parallelschaltungen doch Q=Q1+Q2 sein muss?
Wieso also zeigen die Spannungspfeile der Ersatzpannung in gegensätzliche Richtungen?
Hier die Lösung:
https://i.gyazo.com/7849a750bdf216a363a5796b1ab5d84d.png
Grüße und Danke
Kann mir jemand erklären, warum im Zustand S = zu die Kondensatoren C1 und C2 parallel zu C3 geschalten werden?
Weil der Kondensator C3 parallel zur Reihenschaltung aus C1 und C2 liegt. Ist halt so.
Warum gilt dann U12 = (C1U1 - C2U2)/(C1+C2) mit U = Q/C und nicht U12 = (C1U1 + C2U2)/(C1+C2) da bei Paralellschaltung ja gilt Qges = Q1 + Q2
Irgendwie hab ich das Gefühl, die Lösung sei falsch.
Warum sollte noch Energie in den Kondensatoren zurückbleiben?
Auch die zwei seriegeschalteten C1 und C2 werden ja durch den Widerstand "kurzgeschlossen", geben also ihre Energie ab.
Somit wäre die Energie die Summer aller drei Energien (U^2*C/2).
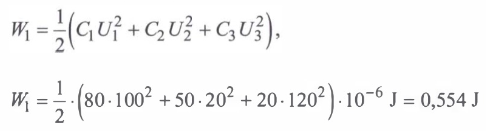
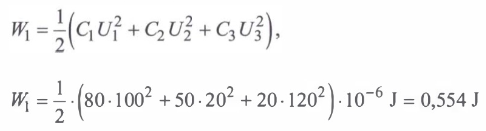
Nein, die Lösung ist OK: du vergisst, dass der Entladevorgang aufhört sobald am Widerstand U3=0 ist:
Dann ist U1'=53,8V und U2'=-53,8V
Das ist der Endzustand.
Stimmt, sorry dem Fragesteller für die Verwirrung.
C1 und C2 sind ja dann quasi parallel.
Ich habe mir geistig für C1 und C2 eine Ersatzkapazität vorgestellt, die dann auch über R entladen würde... ist natürlich falsch.
Vielen Dank für deine Antwort!
Dass wir den Zeitpunkt betrachten , dass U3=0 und UR = 0. Das heißt zu dem Punkt stellt die Verbindung über R einen Kurzschuss von C2 mit C1 dar und die Verbindung über C3 existiert nichtmehr , Quasi ein unendlicher Widerstand , oder?
Wodurch sich eine Parallelschaltung aus C2 und C1 einstellt deren Spannung parallel gegen „Masse“ zeigen, wodurch in deren Masche gilt U1 - U2 = 0 und somit das negative Vorzeichen bei den Ladungen entsteht, da gilt Q=C*U.
Ich glaube ich habs jetzt verstanden, Vielen Dank!