Sinus und Kosinus wie berechnet man 3a?

4 Antworten

seifreundlich2
30.05.2020, 11:02

Der Sinussatz lautet

sin alpha / a = sin beta / b = sin gamma / c

Die Seiten liegen gegenüber des jeweiligen Winkels.

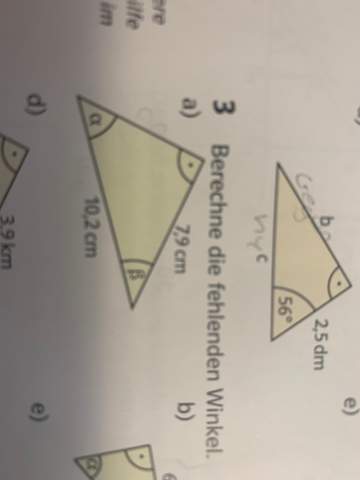
Du hast drei Angaben gegeben, nämlich a = 7.9 cm, c = 10.2 cm und gamma als den rechten Winkel.

Also benutzt du hier die Beziehung

sin alpha / a = sin gamma / c,

löst sie nach sin alpha auf und wendest zum Schluss den ‚arcus sinus‘ darauf an, und schon hast du dein Ergebnis gefunden!
Rhenane
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
30.05.2020, 10:55

einfach die Formeln für sinus und cosinus anwenden...

sin(Winkel)=Gegenkathete/Hypotenuse

cos(Winkel)=Ankathete/Hypotenuse

bezüglich des Winkels alpha ist die Gegenkathete bekannt, also sin nutzen; für beta hast Du die Ankathete gegeben, also cos.

(die Formeln funktionieren natürlich nur bei rechtwinkligen Dreiecken, da es bei allen anderen keine Katheten bzw. Hypotenuse gibt...)
derButterkeks
30.05.2020, 11:49

Dein Dreieck ist Rechtwinklig, also gelten folgende Regeln:

sin(α) = a/c

cos(β) = a/c

Das heißt:

arcsin(a/c) = α #weil der Arkussinus den Sinuswert von α zum Winkelwert umwandelt.

arccos(a/c) = β #weil der Arkuskosinus den Kosinuswert zum Wikelwert unwandelt.

Wenn du das in deinem Taschenrechner eingibst, erhälst du die Winkelwerte. Falls du nicht mit arcsin etc anfangen kannst, musst du in deinem Tachenrechner sin^-1, und cos^-1 eingeben. Das ist dann einfach eine andere Schreibweise.
Hollowpoint
30.05.2020, 10:49

Rechtinkliges dreieck also kannst du den Satz des Pythagoras nehmen, je nachdem noch umstellen