Satz des Pythagoras wenn nur eine Seite gegeben ist
Nein, ich brauch das für keine Hausaufgabe, da ich sowieso Ferien habe. Aber ich dachte mir grade ich lern mal ein bisschen Mathe und da seh ich eine Aufgabe, die mir unmöglich scheint, da nur die Hypotenuse gegeben ist.
Wenn es euch nichts ausmacht schreibe ich die Textaufgabe.
Die Seiten eines 19-Zoll-Bildschirmes (die Hypotenuse, da Diagonale, 19 Zoll= 48,26cm) stehen zueinander im Verhältnis 5:4. Wie hoch und wie breit ist der Bildschirm in Zentimetern.
Ihr müsst mir die Aufgabe auch nicht unbedingt lösen, ich brauch nur einen Gedankenanstoß, wie ich solche Aufgaben in Zukunft lösen kann (also wenn z.B. nur die Hypotenuse gegeben ist und sonst nur ein Verhältnis)
Danke im Voraus!

6 Antworten
Im Grunde hast Du 2 Gleichungen mit 2 Unbekannten. Die erste ergibt sich aus dem Satz des Pythagoras:
I. a² + b² = 19²
Die zweite ergibt sich Durch das gegebene Seitenverhältnis:
II. a/b = 5/4Jetzt kannst Du z. B. II. nach a umstellen (a = 5b/4) und das in I. einsetzen. Das ergibt eine quadratische Gleichung in einer Unbekannten:
(5b/4)² + b² = 361Noch ein bisschen ausmultiplizieren, zusammenfassen, umstellen und normieren, dann kannst Du die z. B. mit p-q-Formel lösen.
Alternativ funktioniert natürlich auch die Lösung von AgentHornet sehr gut.
Man weiss, dass...
...der Bildschirm eine Diagonalenlänge von 19 Zoll = 48,26 cm hat
...die Breite des Bildschirmes um 1/4 länger als die Höhe des Bildschirmes ist
jetzt kannst du eine Gleichung mit Pytagoras machen.
x = Höhe des Bildschirmes
√((5x/4)^2+ (1x/4)^2 ) = 48,26 (siehe Bild)
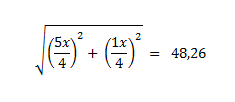
Du kennst das Verhältniss von den beiden Katheten a und b. Du kannst also folgende Gleichung aufstellen: a^2+b^2=c^2 => 48,26^2 = (5X)^2 + (4X)^2. Jetzt kannst du einfach nach X auflösen und dann ist die Höhe gleich 4X und die Breite gleich 5X.
Sinus und Kosinus eines Winkels sind gegeben über Kathete bzw. Ankathete durch die Hypothenuse. Der Tangens ist auch gegeben als Sinus durch Kosinus. Da du das Verhältnis aus Kathete und Ankathete gegeben hast kannst du dann über den Tangens den Winkel alpha (oder beta, je nachdem) bestimmen.
Ich würde über das Verhältnis herangehen. Egal in welchem Maßstab du es vergrösserst, das Verhältnis würde immer gleich bleiben.
Daher würde ich das die Diagonale für einen Bildschirm mit den Maßen 5 x 4 cm berechnen. Die Diagonale des in der Frage gesuchten Bildschirmes durch die Diagonale des Bildschirmes 5 x 4 teilen und die Verhältnisse 5 und 4 mit diesem durch die Division gewonnenen Faktor multiplizieren. Daraus ergeben sich dann die tatsächlichen Seitenlängen.
Bei einem Bildschirm im Verhältnis 5:4 sind die Verhältnisse der einzelnen Seiten zueinander immer gleich. Verdoppelt sich die Diagonale, verdoppeln sich auch die Seitenlängen. Verdreifacht sich die Diagonale, verdreifachen sich auch die Seitenlängen usw.
Aus den Seitenlängen 5 und 4 kannst du eine Diagonale berechnen. Die Diagonale deines Bildschirmes geteilt durch die vorhin berechnete Diagonale aus den Seitenlängen 5 und 4 ergibt den Faktor, um den dein tatsächlicher Bildschirm grösser ist, als das imaginäre Modell 5:4
Sorry ich versteh gar nichts :D