Polynomfunktion 4. Grades aufstellen Bsp. 3.72b)?
Hallo ich muss zum bsp 3.72) b) eine termdarstellung der polynomfunktion 4. grades machen. ich weiss ich brauch bedingungen, aber kann das irgendwie nicht lösen. kann mir jemand helfen?

3 Antworten
Ansatz:
f(x) = ax^4 + bx^3 + cx^2 + dx + e
Ohne großen Aufwand lässt sich e ermitteln:
f(0)= 4 => e = 4
Es sind 3 Extrema gegeben, also müssen wir mit der Ableitung arbeiten:
f'(x) = 4ax^3 + 3bx^2 + 2cx + d
Daraus lässt sich ohne großen Aufwand d ermitteln:
f(0) = 0 => d = 0
Es bleibt also übrige:
f'(x) = 4ax^3 + 3bx^2 + 2cx
Da setzen wir die weiteren bekannten Bedingungen ein:
f'(2) = 0 => 0 = 32a + 12b + 4c
f'(3) = 0 => 0 = 108a + 27b + 6c
f(2) = 0,8 => 0,8 = 16a + 8b + 4c + 4
Nun haben wir ein LGS mit 3 Unbekannten und 3 Gleichungen, was folglich lösbar ist:
32a + 12b + 4c = 0
108a + 27b + 6c = 0
16a + 8b + 4c = -3,2
Da gibt es nun verschiedene Verfahren. Es kommt aber immer raus:
a = -0,3
b = 2
c = -3,6
Lösung:
f(x) = -0,3x^4 + 2x^3 - 3,6x^2 + 4
Probe mit einem Funktionsplotter:

Das haut hin.
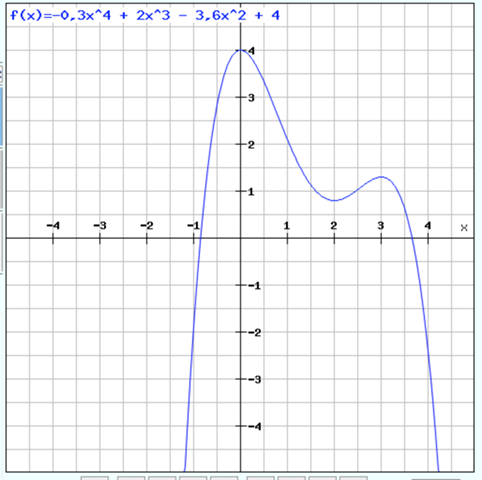
Wie wäre es wenn du die markanten Punkte der Funktion verwendest? Also Nulldurchgang, Maximum bei x = 0, Minimum bei x = 2, f(2) = 0,8, Maximum bei x = 3? Das sind 5 Bedingungen, die für eine Funktion vierten Grades genau ausreichen.
Bedingungen:
f(0) = 4
f'(0) = 0
f(2) = 0,8
f'(2) = 0
f'(3) = 0
Wenn die Funktion lautet:
f(x) = a * x⁴ + b * x³ + c * x² + d * x + e
mit der Ableitung:
f'(x) = 4 * a * x³ + 3 * b * x² + 2 * c * x + d
Dann ist offensichtlich:
e = 4
d = 0
Übrig bleibt ein LGS mit 3 Gleichungen und 3 Unbekannten.
danke, so weit war ich auch aber dann war ich mir nicht sicher weil ich nicht mehr wusste wie ich das löse. was ich bisher herausgefunden hätte ist: f=4 und d=0