Obersumme Integral Grenzwert?

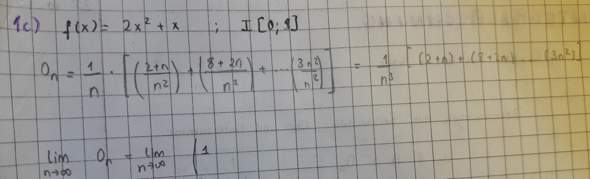
Wie kann ich die Obersumme für die Funktion

f(x) =2x^2 +x mit I[0;1]

und ihren Grenzwert berechnen?

Answer 1

[Ellejolka]

nach der 1. Zeile kommt das;

Comments

[jaykee07]

Vielen Dank😢😢💓

[Ellejolka]

dann

2/n³ •[ n(n+1)(2n+1)/6 + n²(n+1)/4]

dann Klammer lösen

n(n+1)(2n+1)/(3n³) + (n+1)/(2n)

dann

(n/(3n) • (n+1)/n • (2n+1)/n + 1/2 + 1/(2n)

dann

1/3 • (1 + 1/n)(2 + 1/n) +1/2 + 1/(2n)

limes n → unendlich

2/3 + 1/2 = 1 1/6 = 7/6

Answer 2

[ReimundAcker]

Fortsetzung meiner vorhergegangenen Antwort:

$...\ =\frac{2}{n^3}\cdot\frac{n\left(n+1\right)\left(2n+1\right)}{6}+\frac{1}{n^2}\cdot\frac{n\left(n+1\right)}{2}$ $=\frac{1}{n^2}\cdot\left(n+1\right)\cdot\frac{1}{6}\cdot\left[2\left(2n+1\right)\ +\ 3n\right]$ $=\frac{1}{6}\left(\frac{1}{n}+\frac{1}{n^2}\right)\left(7n+2\right)$ $=\frac{1}{6}\left(7+\frac{2}{n}+\frac{7}{n}+\frac{3}{n^2}\right)\ \to\frac{1}{6}\left(7+0+0+0\right)=\frac{7}{6}\ für\ n\to\infty.$

Bitte nachrechnen.

Woher ich das weiß: Studium / Ausbildung – LMU München, Dipl. Math., eigene Recherche

Comments

[jaykee07]

Dankeschönnn❣

Answer 3

[Ellejolka]

O = 1/n • [2•(1/n)²+1/n + 2•(2/n)²+2/n +.............+ 2•(n/n)²+n/n]

jetzt kommt langes Rechnen, Ausklammern, Formeln benutzen, Limes anwenden etc

rauskommen am Schluss muss 7/6

Comments

[jaykee07]

Wie kommst man auf 1^2 + 2^2 +... n^2 in diesem Fall? Ich kenne die Formeln aber ich finde es unmöglich , 2*(1/n)^2 +1/n usw. auszuklammern

[Ellejolka]

du brauchst die Formeln für 1+2+3+....+n

und für 1²+2²+3³+...+n²

[jaykee07]

ich komme mit Ausklammern nicht klar :(

[DerRoll]

@jaykee07

Das ist allerdings ein Problem. Dann solltest du das üben. Denn das Rechnen mit Termen ist eine DER wesentlichen Grundlagen um höhere Mathematik betreiben zu können. Das mußt du im Schlaf beherrschen. Sorry, da kann dir keiner helfen ausser du selbst.

Answer 4

[ReimundAcker]

$O_n=\frac{1}{n}\cdot\left[2\left(\frac{1}{n}\right)^2+\frac{1}{n}\ +\ 2\left(\frac{2}{n}\right)^2+\frac{2}{n}\ +...\ +2\left(\frac{n-1}{n}\right)^2+\frac{n-1}{n}\ +\ 2\left(\frac{n}{n}\right)^2+\frac{n}{n}\right]$ $=\frac{1}{n}\left[2\left(\frac{1}{n}\right)^2+2\left(\frac{2}{n}\right)^2+...+2\left(\frac{n-1}{n}\right)^2+2\left(\frac{n}{n}\right)^2\right]\ +$ $\ +\frac{1}{n}\left[\frac{1}{n}+\frac{2}{n}+...+\frac{n-1}{n}+\frac{n}{n}\right]$ $=\frac{1}{n}\left[\frac{2}{n^2}\cdot1^2+\frac{2}{n^2}\cdot2^2+...+\frac{2}{n^2}\cdot\left(n-1\right)^2+\frac{2}{n^2}\cdot n^2\right]\ +$ $\ +\frac{1}{n}\left[\frac{1}{n}\cdot1+\frac{1}{n}\cdot2+...+\frac{1}{n}\cdot\left(n-1\right)+\frac{1}{n}\cdot n\right]$ $=\frac{1}{n}\cdot\frac{2}{n^2}\cdot\left[1^2+2^2+...+\left(n-1\right)^2+n^2\right]\ +$ $\ +\frac{1}{n}\cdot\frac{1}{n}\cdot\left[1+2+...+\left(n-1\right)+n\right]$

= ...

Fortsetzung in meiner nächsten Antwort (wegen Speicherproblem von gf gesplittet).

Woher ich das weiß: Studium / Ausbildung – LMU München, Dipl. Math., eigene Recherche

Comments

[jaykee07]

Vielen Dank♡♡♡