Momentane Beschleunigung?

Bei der Aufgabe wäre wirklich Hilfe sehr cool, weil ich mit den Tangenten sehr unsicher bin. Danke! Alle anderen Aufgaben habe ich schon alleine gemacht, deswegen

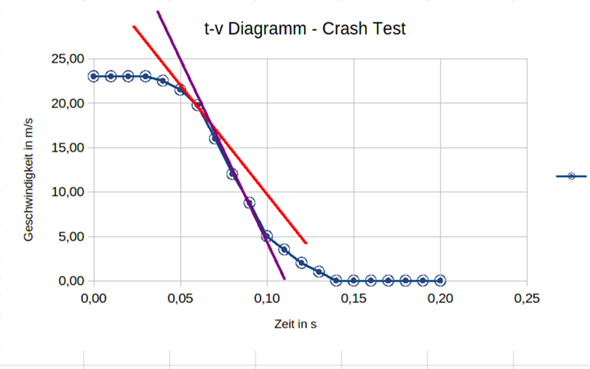
Bei einem Crashtest (- Abb. 2) wurde das v(t)-Diagramm in Abb. 4 aufgezeichnet.

Aufgabe: Bestimmen Sie die momentanen Beschleunigungen für die Zeitpunkte

t = 0,07s, t = 0,08 s, t = 0,09 s, t = 0,10 s und t = 0,11s. Zeichnen Sie dazu Tangenten

an den Graphen und bestimmen Sie jeweils die Steigung.

Answer 1

[DrNumerus]

Das ist immer etwas ungenau, wenn man das händisch anhand von solchen diskreten Diagrammen ermitteln soll. Allerdings sind in dem Plot ja die Geschwindigkeiten in einem gleichmäßigen Abstand von 0,01s dargestellt. Das kann man sich zu nutze machen zusammen mit der Annahme, dass sich die Geschwindigkeitskurve recht "schön" verhält. Dazu würde ich vorschlagen, die Tangente am Zeitpunkt i über die Verbindung von Punkt i-1 und i+1 zu berechnen, also

$a_i=\frac{v_{i+1}-v_{i-1}}{0,02\ s}$

Da du nicht weißt was zwischen den Punkten genau passiert, ist das wohl eine erste gute Näherung. Wenn der eine Punkt am Zeitpunkt i nämlich deutlich außerhalb von der Verbindung von i-1 und i+1 liegt, so muss die Kurve ja insgesamt an der Stelle auch "ausbeulen" und hätte etwa in der Mitte die Steigung, die auch die Verbindung von i-1 und i+1 hätte, da es quasi eine rotierte Version ist von sowas:

Die gesuchten Punkte sind durch geometrische Skalierungen meiner Meinung nach etwa:

$P_1\left(0,07\ s\ ;\ 15,74\ \frac{m}{s}\right)$

$P_2\left(0,08\ s\ ;\ 12,2\ \frac{m}{s}\right)$

$P_3\left(0,09\ s\ ;\ 9,39\ \frac{m}{s}\right)$

$P_4\left(0,1\ s\ ;\ 5\ \frac{m}{s}\right)$

$P_5\left(0,11\ s\ ;\ 3,64\ \frac{m}{s}\right)$

Mit meiner vorgeschlagen Methode braucht man dann noch den vorangehenden und nachlaufenden Punkt:

$P_0\left(0,06\ s\ ;\ 19,47\ \frac{m}{s}\right)$

$P_6\left(0,12\ s\ ;\ 2,22\ \frac{m}{s}\right)$

Damit wäre die Steigung der Tangente an den ersten Punkten:

$a_1=\frac{12,2\ \frac{m}{s}-19,47\ \frac{m}{s}}{0,02}=-363,5\ \frac{m}{s^2}$

$a_2=\frac{9,39\ \frac{m}{s}-15,74\ \frac{m}{s}}{0,02\ s}=-317,5\ \frac{m}{s^2}$

$a_3=\frac{5\ \frac{m}{s}-12,2\ \frac{m}{s}}{0,02\ s}=-360\ \frac{m}{s^2}$

und so weiter...

Woher ich das weiß: Studium / Ausbildung – Physik Studium - Master in theoretischer Physik

Answer 2

[verreisterNutzer]

Ich kann da im Rahmen der Genauigkeit eigentlich nur 2 Tangenten sinnvoll bist t=0,10 einzeichnen (die Tangente für t=0,11 findest Du nun sicher selbst)

Answer 3

[SevenOfNein]

Die Tangente an einem Punkt, ist eine Gerade, die durch den Punkt geht, bzw. knapp anliegt. UND die Steigung der Kurve in dem Punkt am Besten abbildet. Du musst erstmal die Punkte möglichst elegant so miteinander verbinden, dass eine schöne Kurve ohne Ecken und Kanten rauskommt. Und dann die Tangente, Gerade am Punkt so einzeichnen, damit die möglichst viel der Kurve in unmittelbarer Nähe des Punktes bedeckt. ODER in unmittelbarer Nähe des Punktes in etwa gleich viel Abstand zur Kurve hat. Schwer zu erklären..