Minimax Aufgabe/ Extremwert Aufgabe kann mir das einer erklären?
Hallo, ich bind er Timo und aus aHamburg. Wir schreiben bald eine Mathearbeit.
Ich sitze schon so lange an dieser Aufgabe, aber komme einfach nicht auf die Lösung.
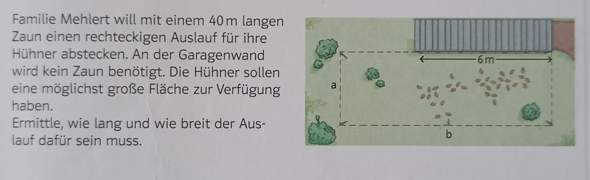
Wenn bei der Aufgabe nicht nur an einem Teil der Seite der Schuppen wäre, sondern an der ganzen Seite, könnte ich sie lösen. Aber ich hab überhaupt keine Iden mehr, was ich noch machen kann. Hat einer von euch eine Idee?
Am besten wäre es, wenn ihr es mir mit dem Verfahren mit der Ableitung erklären könntet.
Vielen Dank schonmal
3 Antworten
Die Fläche A = a*b soll so groß wie möglich sein .
.
Als Nebenbedingung nutzt man die 40 Meter vorgegebene Länge, den Umfang
(Teil vom Schuppen ? (b-6) !!! )
U = a + b + a + (b-6) = 2a + 2b - 6 = 40
=
2a + 2b = 46
.
Auflösen nach a oder b ( egal)
ich nehme a
a = (46-2b)/2
a = 23 - b
.
Jetzt wird
A(b) = (23-b) * b gebildet
A(b) = 23b - b²
Ableiten
A'(b) = 23 - 2b
gleich Null setzen
0 = 23 - 2b
-23/-2 = b = 11.5
.
Weil A''(11.5) = -2 ist , ist 11.5 tatsächlich max.
.
Jetzt noch a mit
2a + 2*11.5 = 46
2a = 46 - 23
a = 23
.
A_max ist daher 11.5 * 23 = 230 + 23 + 23/2 = 264.5 m²
.
(I) 40 = 2a + 2b - 6 ; (II) A = ab ;
Löse Gleichung (I) nach b auf und setze dies in Gleichung (II) ein !
Differenziere dann A nach a und setzte dies Null !
Zaunlänge:
40 = 2a + 2b - 6
Fläche:
A = ab
Hilft das?
Löse 40 = 2a + 2b - 6 nach a oder b auf und setzt es in A = ab ein. Du erhältst ein quadr. Gleichung, deren Maximum du bestimmst.
Wenn a und b Grenzwerte haben, dann wird das Produkt beider Zahlen am größten, wenn beide gleich groß sind.
Entsprechend könntest du für diese Aufgabe folgendes ableiten:
2a + 2b = 4a
SebRmRs Methode führt dich korrekterweise zum Maximum, was dich anschließend darauf bringt, dass a und b gleich groß sind.
Aber wenn ihr gerade mal bei Flächenberechnungen seid, wirst du vermutlich nicht die Extremwerte eine Funktion bestimmen können, oder?
Das hatten wir letztens, extremwerte mit Funktionen, aber ich finde es mit ableitungen einfacher
Na, dann kannst du es doch nach SebRmRs Anleitung berechnen.
40 = 2a + 2b - 6 | + 6
46 = 2a + 2b | : 2
23 = a + b | - b
a = 23 - b
........
A = ab
A = (23-b)b
A = 23b - b²
Ableiten und Extremwert bestimmen:
23 - 2b = 0 | -23
-2b = -23 | : (-2)
b = 11,5
Jetzt kannst du b in der Eingangsgleichung mit 11,5 ersetzen:
40 = 2a + 2b - 6
46 = 2a + 2*11,5
46 = 2a + 23 | - 23
23 = 2a | : 2
a = 11,5
Ne, nicht wirklich, kann du mir das vielleicht irgendwie genauer erklären?