Mathe pq Formel was falsch?

Hey,
was habe ich bei dieser Aufgabe falsch gemacht? Tut mir leid wegen meiner Schrift.
Danke im voraus!
7 Antworten
Du hast die 1. binomische Formel falsch angewandt.
(Die Schrift ist lesbar, und Du hast das Bild auch lesbar eingestellt. :) )
Aber bitte nicht bei der p-q-Formel anwenden, dann veränderst du p und q in der Ausgangsformel und kannst die p-q-Formel nicht mehr anwenden!
Aber bitte nicht bei der p-q-Formel anwenden, dann veränderst du p und q in der Ausgangsformel und kannst die p-q-Formel nicht mehr anwenden!
In der Ausgangsgleichung sind weder p noch q gegeben.
Die hat man erst nach dem korrekten Auflösen des Binoms.
Nein eben nicht.
Dann lös doch mal die quadrierte Klammer auf und bring die Gleichung in die Normalform.
Da wirst überrascht sein. :)
also ich meine, dass die Ergebnisse, wenn man etwas in der Klammer auflöst falsch wären
y=x^2+x+1+4
y=x^2+x+5
Naja, ich spendiere Dir noch ein weiteres x. Du weiß schon, ... +2AB ...
y = x² + 2x + 5
Und bei q kommst Du jetzt ja auch auf die richtige 5 und nicht mehr auf die 4. :)
Danke für das weitere x, da war die Konzentration wegen eines schreienden Babys schon woanders. Ich habe beim Insbettbringen meiner Kinder gerade etwas Zeit gehabt, um in meinen verstaubten Erinnerungen zu wühlen. Und du hast Recht. Ich hab das mit ner anderen Regel durcheinandergebracht >.< Da rief es dann gerade im Kopf: "Nullstellen mit der p-q-Formel kann man nur berechnen, wenn das x² gegeben ist." Dann darf man aber p und q erst angeben, wenn die Gleichung mit y=x²+x+c gegeben ist, also y=x²+ax+c und dann ist p=a und q=c.
Ich hoffe mein Fehler wird noch rechtzeitig vom Fragesteller gelesen!
Kein Problem.
Der Fragesteller hat sich ja für diese richtige Antwort bedankt: https://www.gutefrage.net/frage/mathe-pq-formel-was-falsch#answer-323052232, und wird damit wohl auch gut weiterkommen.
Wünsche Dir einen angenehmen Abend. :)
Die Schrift ist lesbar, das ist kein Problem.
Ich würde gar nicht erst die Klammer ausmultiplizieren, sondern direkt auf beiden Seiten mit -4 subtrahieren
jetzt würde ich radizieren
Ein möglicher Antwortsatz wäre jetzt:
Für das Radizieren einer Zahl x < 0 gibt es keine reelle Lösung
und dann wäre auch schon Schluss mit dem "kurzen Abenteuer". Da in der Schule x stets ein Element der reellen Zahlen ℝ ist.
Bei deinem Rechenweg ist offenkundig falsch, dass du (x+1)² falsch ausmultipliziert hast, nach der 1. binom. Formel gilt
und auf dein Beispiel angewandt
Quadratische Gleichungen löst man nicht mit einer Formel, sondern über die quadratische Ergänzung!
(x+1)² + 4 =y
(x+1)*(x+1)+4=y
x²+x+x+1+4=y
x²+2x+5=y
Bei Dir fehlt 1x und 1. Du hast nur (x+1)*x gerechnet.
Bei den Kommentaren kann ich das Bild irgendwie nicht einfügen, deswegen jetzt so.
oben wie man eine binomische Formel auflöst. Unten warum es nicht geht die aufgelöste binomische Formel für die p-q-Formel zu benutzen.
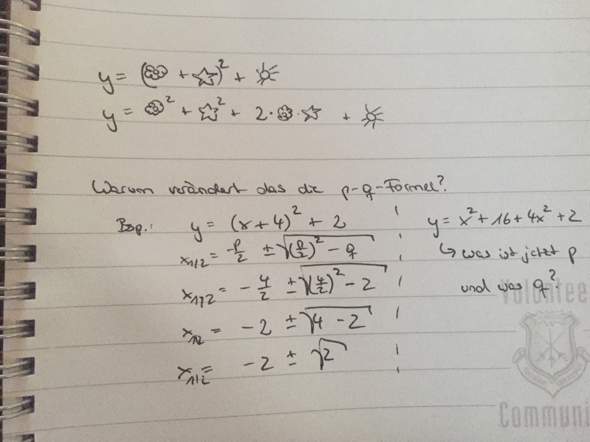
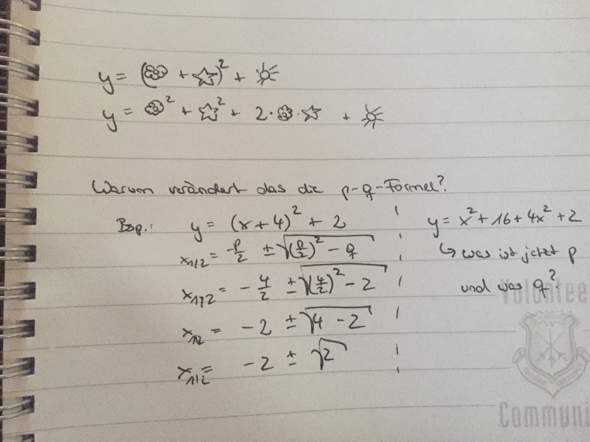
Wie wendet man sie denn richtig an^^?
Danke