Mathe frage (Funktionen)?
Die Aufgabe lautet:
1) Begründe, dass die Gerade f mit f(x) = 4x +5 parallel zur Geraden g mit g(x) = 4x +1 verläuft.
2) Berechne anschließend den Abstand der beiden Geraden.
Wie berechne ich den Abstand?
4 Antworten
Zur Berechnung des Abstandes habe ich folgenden Vorschlag:
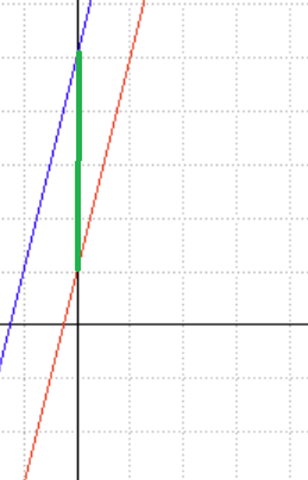
Zeichne die Geraden f(x) und g(x) in ein Koordinatensystem.
Der Schnittpunkt von g mit der y-Achse sei A, der Schnittpunkt von f mit der y-Achse sei B.
Zeichne eine Parallele zur x-Achse bei y=1 (also durch A). Ihr Schnittpunkt mit f sei C.
Die Länge der Streche AB ist 4. Da der Anstieg der beiden Geraden 4 ist, ist die Länge der Strecke AC = 1.
Nach Pythagoras ist die Länge der Strecke BC = Wurzel(17).
Nun hat das Dreieck ABC den Flächeninhalt AC * AB / 2. Wenn man BC als Grundseite betrachtet, auf der die Höhe h steht, ist der Flächeninhalt auch BC * h / 2.
Daraus folgt h * Wurzel(17) = AC * AB = 4.
h = 4 / Wurzel(17) ist der gesuchte Abstand der Geraden.
- kann man nicht begründen, weil es falsch ist. Entsprechend kann man
- keinen Abstand angeben.
Hast du die Aufgabe richtig abgeschrieben?
Wie berechne ich den Abstand?
Du wählst einen Punkt auf einer der beiden Geraden, bestimmst die Normale in diesem Punkt und ihren Schnittpunkt mit der anderen Geraden. Anschließend bestimmst du den Abstand dieser beiden Punkte mit der Formel
vgl. https://www.youtube.com/watch?v=PFN8e5mVHDc
Leider sind die Zahlen etwas krumm, am Ende habe ich
ca. 0,97
Bei dieser Aufgabe kommt es darauf an, was du als Abstand definierst. Ich habe dir einfach mal 2 Beispiele aufgezeigt:
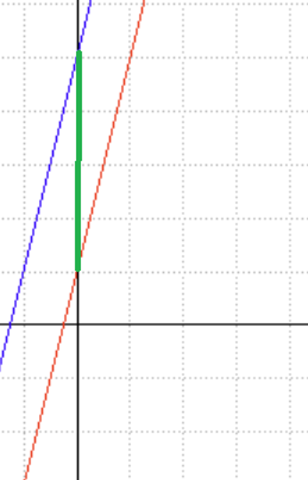
Ist das der Abstand gilt ganz einfach: A(x)=f(x)-g(x)=4.
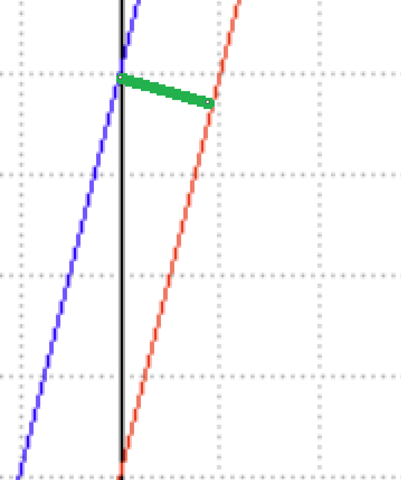
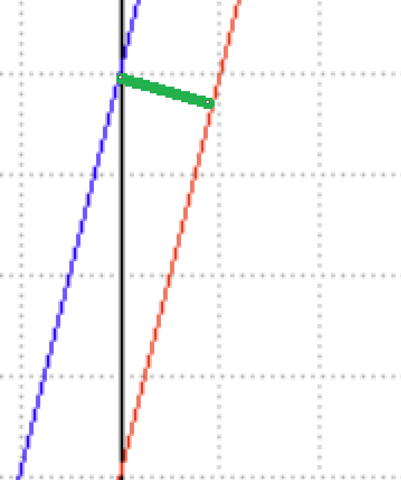
gilt das als Abstand, also die rechteckige Verbindung, muss man etwas überlegen, um eine kluge, simple Lösung zu finden. Hier gilt: Viele Wege führen nach Rom, einer funktioniert mit dem Ansatz, dass ein zu dem Anstieg m senkrechter Anstieg gleich -1/m ist. In dem Fall also -1/4. Die Gerade soll außerdem durch (0/5) gehen.
Wir erhalten also: y=-1/4x+5 und können jetzt beide Schnittpunkte suchen
-1/4x+5=4x+5 <-> x=0, y=5
-1/4x+5=4x+1
17/4x=4
x=16/17, y=81/17
Abstand der Punkte: ca. 0,97LE