Kann mir bitte jemand die Matheaufgabe Nummer 12 lösen?
2 Antworten
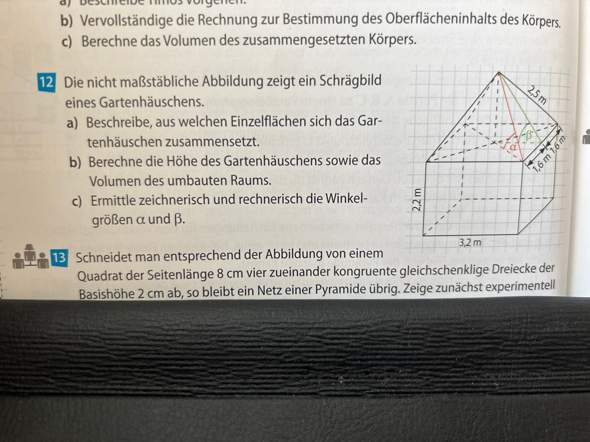
Aufgabe 12a
Das Gartenhäuschen besteht aus
1 Quadrat (Boden)
4 Rechtecke (Wände)
4 Dreiecke ( Dach)
------------
Aufgabe 12b
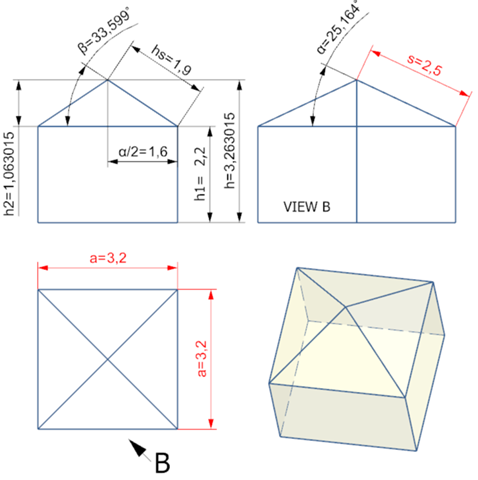
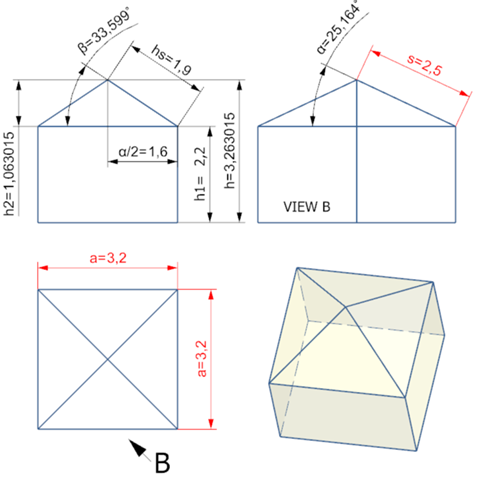
Berechnung Pyramide h2
Gesucht: Körperhöhe h2
Gegeben: a = 3,2 m
Gegeben: s = 2,5 m
---
h2 = Wurzel( s² - ( (Wurzel(2) * a) / 2 )² )
h2 = Wurzel( 2,5^2 - ( (Wurzel(2) * 3,2) / 2 )^2 )
Körperhöhe h2 beträgt 1,063015 m
---
Höhe Gartenhäuschen h
h = h1 + h2
h = 2,2 + 1,063015
h = 3,263015 m
------
Volumen Quader V1
V1 = a² * h1
V1 = 3,2^2 * 2,2
V1 = 22,528 m³
---
Volumen Pyramide V2
Gesucht: Volumen V2
Gegeben: a = 3,2 m
Gegeben: h2 = 1,063015 m
---
V2 = (1/3) * a² * h2
V2 = (1/3) * 3,2^2 * 1,063015
Volumen V2 beträgt 3,628425 m³
---
Volumen Gartenhäuschen
V = V1 + V2
V = 22,528 + 3,628425
V = 26,156 m³
------------
Aufgabe 12c
Berechnung d
Gesucht: Diagonale d
Gegeben: a = 3,2 m
---
d = Wurzel( a² + a² )
d = Wurzel( 3,2² + 3,2² )
Diagonale d beträgt 4,525483 m
---
Gesucht: Winkel α
Gegeben: d = 4,525483 cm
Gegeben: h = 1,063015 cm
---
α = arctan( h / (d/2) )
α = arctan( 1,063015 / (4,525483/2) )
Winkel α beträgt 25,164°
---
Berechnung β
Gesucht: Winkel β
Gegeben: a = 3,2 cm
Gegeben: h = 1,063015 cm
---
β = arctan( h / (a/2) )
β = arctan( 1,063015 / (3,2/2) )
Winkel β beträgt 33,599°
Nr.12a:)(a^2)+4×a×b+2×a×sqrt((c^2)-((a÷2)^2))
=(3.2^2)+4×3.2×2.2+2×3.2×sqrt((2.5)^2-((3.2÷2)^2))
b:) h = b + sqrt((c^2)-(a÷(2×(sqrt(2)))^2))
= 2.2 + sqrt((2.5^2)-(3.2÷(sqrt(8))^2))
V = (a^2)×b+(a^2)×(b + sqrt((c^2)-(a÷(2×(sqrt(2)))^2)))÷3
=(3.2^2)×2.2+(3.2^2)×(2.2 + sqrt((2.5^2)-(3.2÷(sqrt(8))^2)))÷3
c:)cos(alpha) = a÷sqrt(8)÷c |×arccos(...)
Alpha = arccos(a÷sqrt(8)÷c)
Alpha = arccos(3.2÷sqrt(8)÷2.5)
cos(beta) = sqrt((c^2)-((a÷2)^2)) ÷ (-a÷2) |arccos(...)
Beta = arccos(sqrt((c^2)-((a÷2)^2)) ÷ (-a÷2))
Ich bin immer für Fragen und Kritik offen.
cos(beta) = sqrt((c^2)-((a÷2)^2)) ÷ (a÷2) |arccos(...)
Beta = arccos(sqrt((c^2)-((a÷2)^2)) ÷ (a÷2))
Beta = arccos(sqrt((2.5^2)-(3.2÷2)^2÷(3.2÷2))
vielen dank!!