Lokale Extremstellen am Rand der Definitionsmenge?
Hallo,
ich habe 2 Fragen zu Extremstellen bei reellen Funktionen
1.) Ist eine Extremstelle (sowohl lokal als auch global) am Rand der Definitionsmenge möglich?
z.B.:
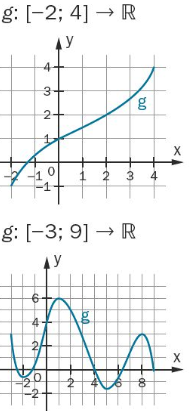
In dem ersten Beispiel sind -2 und 4 globale Extremstellen, korrekt?
Aber sind sie auch lokale Extremstellen?
2.)
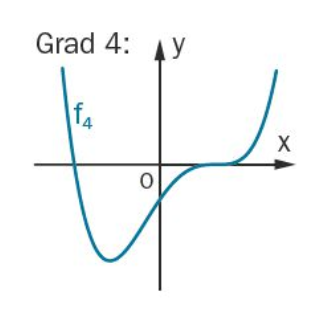
In dem obigen Beispiel ist eine Funktion vierten Grades abgebildet. Diese hat ein globales Minimum, korrekt? Hat sie jedoch 1, 2 oder 3 lokale Extremstellen (die globale Extremstelle wird hier bereits als lokale Extremstelle dazugezählt)?
1 Antwort
1.) Ist eine Extremstelle (sowohl lokal als auch global) am Rand der Definitionsmenge möglich?
In dem ersten Beispiel sind -2 und 4 globale Extremstellen, korrekt?
Aber sind sie auch lokale Extremstellen?

Jap ist sie. -2 und 4 ist sowieso eingeschlossen, siehe Schreibweise Intervall Klammer
Wie du siehst unterscheidet man hier zwischen lokal und global. Dein globales Maximum kann auch ein lokales sein, wenn du dein Anschauungsintervall I entsprechend wählst, also je nach betrachtungsweise.
Siehe https://de.wikipedia.org/wiki/Extremwert
2)
Diese hat ein globales Minimum, korrekt?
Jap und im ganzen Def. Bereich strebt sie links und rechts gegen +inf, daher würde ich behaupten, es gibt kein eindeutiges globales Maximum.

Wenn der Definitionsbereich nicht eingeschränkt ist, dann nicht.
Dann muss man die Randwerte extra betrachten, da dort bei einem Extremum nicht unbedingt eine waagerechte Tangente vorliegen muss. (dein oberes Beispiel)
Ok, vielen Dank. Gibt es im zweiten Bsp. jedoch auch noch weitere lokale Extremstellen (abgesehen von dem globalen Minimum, welches ja auch ein lokales Minimum ist)