Kennt sich jemand in diesem Teilgebiet aus?
Hallo Leute,
Es gibt in der Numerik und bei der Finite-Elemente-Methode gewisse Methoden, mit denen man numerisch differenzieren kann (ableiten). Soweit ich weiß, heißen diese Finite-Differenzen-Methode oder FDM.
Die eigentliche Frage ist deutlich komplizierter. So kompliziert, dass ich sie gar nicht stellen will. Stattdessen möchte ich mich gerne privat mit jemandem darüber austauschen, da ich eine Vermutung habe, die ich nirgendwo bestätigt finden konnte (ich habe auf Google, Wikipedia und Co. gesucht).
Deshalb die Frage:
Kennt sich jemand gut mit der Finite-Differenzen-Methode aus?
Falls ihr von diesem Thema keine Ahnung habt, dann schreibt das doch auch. Es ist okay, wenn man von FDM noch nie etwas gehört hat.:-)
Grüsse R
3 Antworten
Die Finite Differenzen Methode ist nicht die beste Methode. Aber sie funktioniert. Habe damit schon Äquipotenziallinien für elektrostatische Problemstellungen gerechnet. Hier eine Gitterkonstruktion mit 100 Stützstellen. Die roten Punkte stellen die Bewandung einer quadratischen Röhre auf Nullpotenzial dar. Die grünen Punkte befinden sich auf auf dem Niveau von 1V.
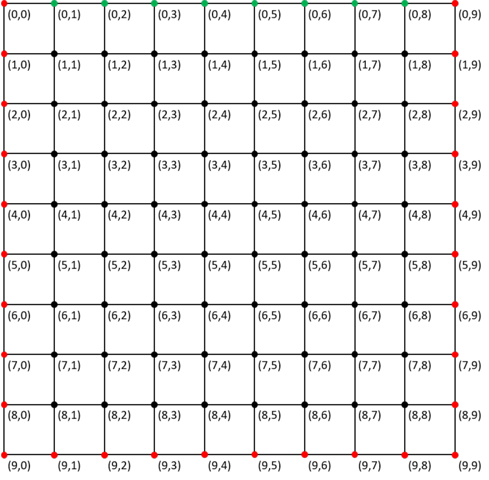
Die Auflösung des zugehörigen Gleichungssystems mit rund 100 Variablen liefert folgendes Feldbild. Es wurde gerechnet mit Octave mit einem Aufwand von rund 90 Zeilen Code.
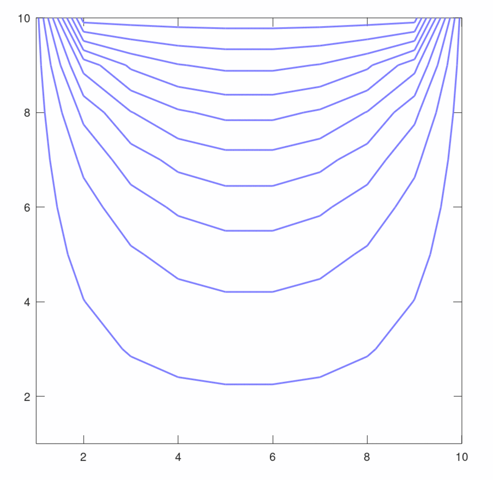
Wer Lust hat kann das sogar mit Excel nachprogrammieren.


Ich habe die Diskretisierung von DGLs und Finite Elemente zwar im Rahmen der Numerik während des Studiums behandelt, das ist aber lange her, so dass ich wohl nicht mehr in der Lage sein werde, sehr spezifische Fragen zu beantworten…
Die Methode der finiten Differenzen ersetzt Differentialgleichungen samt Rand- und Anfangswerte durch lineare Gleichungen, welche numerisch gelöst werden. Im Rahmen des Verfahrens werden Ableitungen einer Funktion durch Differenzenquotienten ersetzt. Was soll daran so kompliziert sein, um es nicht in wenigen Sätzen formulieren zu können?
Rammstein53 wäre es okay wenn ich meine Vermutung mit dir im Privat chat austausche ? Aber so viel sei gesagt um die DLG zu lösen muss man dafür eine Matrix A deffinieren sodass man die Form A x b = w erhält. Jedoch was interessant ist das man die Matrix a Belibig anderst beschreiben kann. Die Vermutung ist vereinfacht gesagt, wie schnell und wie preäsise sich der Fehler verhält wenn ich die Matrix A belibig komlizierter gestallte. (Jekomplizierter die Matrix, desto kleiner wird der Fehler) Hättest du interesse auf Privat CHat darüber zu discutieren ?
Hallo Prof Nick wärst du interessiert über die konkrete Problem stellun auf Privat chat zu discutieren ?