Induktion flächenänderung?
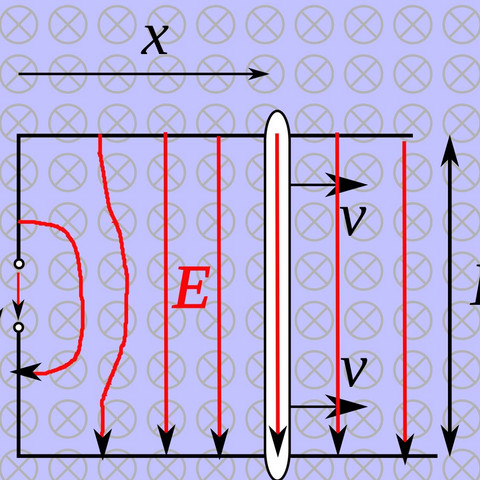
Im Bild sieht man einen geraden Leiter der auf einer Schiene mit der Geschwindigkeit v auf ihr rollt. So jetzt wird ja eine Spannung U induziert. Und die Spannung berechnet sich ja nach U=vBL.
In der dortigen Herleitung wurde diese Formel unter der Annahme einer flächenänderung hergeleitet. Aber meine Frage nun. Gilt das mit der flächenänderung nicht nur für spülen? Denn hier in der Abbildung entsteht ja auch keine geschlossene Windung. Warum geht man dann doch über die flächenänderung ?
Wenn sich ein gerader Leiter ohne Schiene durch ein Magnetfeld bewegt gilt ja dieselbe Formel daher müsste es ja auch egal sein ob die Schiene nun da ist oder nicht.
4 Antworten
Als Ergänzung zu atoemlein:
Das Induktionsgesetz lässt sich in verschiedenen Formen anschreiben, die zueinander mathematisch äquivalent sind. In allen Fällen muss man aber extrem darauf achten in welchem Bezugssystem man sich befindet.
Das Induktionsgesetz besagt in einer Form, dass
das Umlaufintegral über die elektrische Feldstärke im Ruhesystem des jeweiligen Linienelements gleich ist der (negativen) zeitlichen Änderung des magnetischen Flusses durch die betrachtete umrandete Fläche.
Dabei ist es übrigens völlig unerheblich, ob die geschlossene Kontur entlang eines vorhandenen Leiters verläuft oder nicht (damit tun sich besonders Schüler schwer, da das Induktionsgesetz oft ungünstig unterrichtet wird und so getan wird, als wäre elektromagetische Induktion ein Vorgang, der sich nur durch die Lorentzkraft beschreibnen ließe - das ist aber was anderes...). Den geltenden Naturgesetzen ist es "egal", ob da ein Leiter ist oder nicht, und schon ganz egal, ob der Leiter ausieht wie eine technische Spule oder nicht.
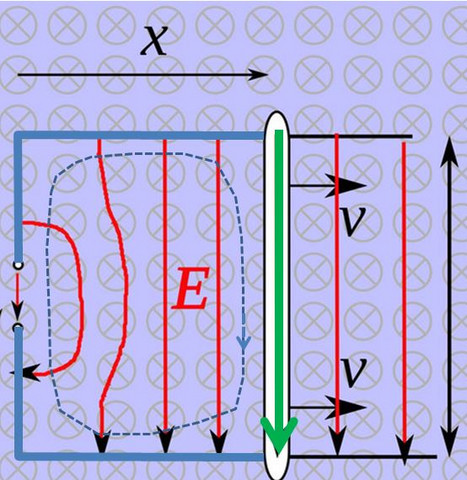
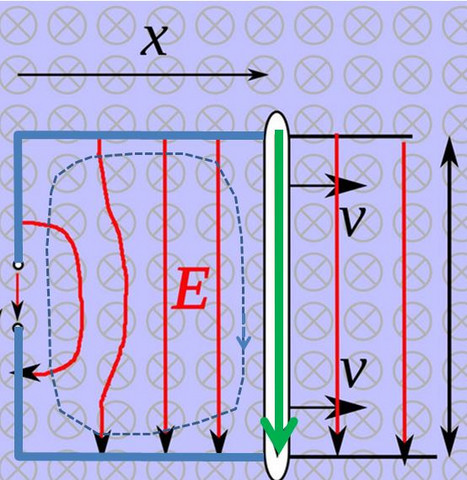
In unserem Fall können wir den Weg aber gerne entlang des Leiters verlaufen lassen: Wenn wir uns die Felder in deinem Bild im Laborsystem aufmalen sehen wir, dass im bewegten Leiter (grün) eine Feldstärke vorhanden ist, in den übrigen Leitern aber keine (blau).
Im mitbewegten System des bewegten Leiters (in seinem Ruhesystem) gibt es aber kein elektisches Feld (kann es ja keines geben, denn ansonsten würden sich die dort ruhenden Ladungsträger ja bewegen - Widerspruch), daher ist das sich ergebende Umlaufintegral gerade die linke Spannung zwischen den Klemmen. Es gibt nicht wenige Lehrbücher, wo dem Aspekt des Bezugssystem nicht Rechnung getragen wird und sich daher etwas seltsame oder scheinbar widersprüchliche Ergebnisse ergeben,wenn man versucht, die entstehende Spannung als Integral über die Feldstärke von Klemme A bis Klemme B zu definieren, aber mit der Feldstärke im Laborsystem arbeitet.
Da in Deinem Fall B konstant ist und sich die Fläche andert
ist die Änderungsrate des magnetischen Flusses
und daher ist das auch die Spannung an den Klemmen.
Ich muss aber zugeben, dass ich das als Teenager auch nicht verstanden habe ;-)
Induktion wird durch Flussänderung, nicht durch Flächenänderung hervorgerufen, bzw. steht mit dieser in einem engen Zusammenhang.
Und da ist doch eine Fläche, nämlich jene, die oben eingezeichnet ist.
In diesem Fall ist es die Fläche, die durch die Leiter aufgespannt wird. Und wenn du das Induktionsgesetz auf diese Fläche anwendest, bekommst du eben die Spannung an den Klemmen. Dass die Schiene weitergeht ist ja egal - es geht um einen geschlossenen Weg und der ist vorhanden.
Ja aber muss die Fläche nicht geschlossen sein zb eine Spule das ist eine geschlossenerer „Kreis“. Hier haben wir oben und unten einen Leiter und rechts den Leiter der rollt. Aber an der linken Seite ist das kein geschlossenes Rechteck ganz profan ausgedrückt und daher keine geschlossene Fläche
Du bildest das Linenintegral von E auf folgendem Weg:
- obere Klemme
- nach oben
- nach rechts
- nach unten
- nach links
- nach oben zur unteren Klemme
- von unterer Klemme zu oberer Klemme
Alle Leiter tragen nichts zum Wegintegral bei, da das Feld im Ruhesystem Null ist. Bleibt nur das Integral der Feldstärke von unterer zu oberer Klemme; das ist aber die Spannung U zwischen den Klemmen.
Also gilt:
U = dϕ/dt, wobei ϕ der Fluss durch die soeben definierte Umrandung ist.
> und daher keine geschlossene Fläche
wie schon gesagt: Es geht um eine gedankliche Fläche mit einem gedanklichen Weg, der diese einschließt.
Das Induktionsgesetz gilt für jede gedanklich mögliche Umrandung, es ist unerheblich, ob da ein Leiter ist oder nicht.
In unserem Fall wählen wir aber die Leiterschleife. Bei der Integration über den offenen Teil (links) bekommt man gerade die Spannung an den Klemmen.
Ok und warum sagt man nicht einfach : wir haben einen bewegten Leiter im b Feld und daraus folgt Fl=Fe
qvB=qU/L
U=LvB
Kommt ja scheinbar auf dasselbe hinaus ist das Zufall ?
Nein, das ist natürlich kein Zufall. Die Spannung an einem Stab kann man aber nur messen, wenn man ein Voltmeter abnschließt. Dieses hat Anschlusskabel und bildet eine Stromschleife, so wie im Beispiel. Atoemlein hat das schon erwähnt.
Die Gkleichungen der Elektrodynamik sind natürlich in sich konsistent, und wenn man die durch die Lorentzkraft entstehende Ladungstrennung im bewegten Leiter betrachtet, muss die entstehende Feldstärke natürlich die gleiche sein, wie jene, die man aus dem Induktionsgesetz dieser obigen Art bekommt.
•es geht um einen geschlossenen Weg und der ist vorhanden.
Er ist doch links zwischen den klemmen offen
> Er ist doch links zwischen den klemmen offen
Der Weg beginnt bei der oberen Klemme, über die Leiter, zur unteren Klemme und dann wieder zur oberen. Das ist doch ein geschlossener Weg!
Das Teil-Integral von der unteren Klemme zur oberen ist
∫ E ds =U
also die Spannung zwischen den Klemmen.
Nochmal: Der Weg muss mathematisch gschlossen sein, es hat nichts damit zu tun, ob da ein Leiter ist oder nicht. ;-)
Schließlich gibt es Induktion ja auch im leeren Raum, wo ein sich änderndes Feld B ein Feld E hervorruft - und da ist gar kein Leiter.
Ok verstanden und worin liegt nun der Unterschied zwischen dieser Schleife und einem einfach Leiter im b Feld ?
Der diffizile Unterschied ist, dass du an einem Stab der sich durch ein homogenes Magnetfeld bewegt ein Spannungsmessgerät anbringen musst, um die Spannung zu messen.
Atoemlein hat das hier schon bemerkt:
...dass man die Spannung nicht am bewegten Stab-Ende abnehmen will und kann, sondern eben (wie in elektrischen Generatoren) irgendwo an einem fixen Anschluss....
Es hängt aber vom Bezugssystem ab, ob das Gerät Spannung anzeigt oder nicht:
Wenn du dich auf den Stab mit dem Voltmeter gedanklich (oder auch real) draufsetzt und die Strippen links und rechts anschließt, wirst du keine Spannung messen. Die Situation ist, dass du dich als Ganzes in einem homogenen elektrischen Feld der Stärke v*B befindest, welches senkrecht zu B und v ist. Die Enden des Stabes werden zwar im Feld polarisiert (so dass im Inneren des Stabes E=0 herrscht), aber natürlich kann das Voltmeter nichts anzeigen: so kannst du die Spannung nicht messen – wie auch? Es gilt der Maschensatz und der metallische Stab ist auf einem Potenzial – somit ist der Potenzialunterschied zwischen seinen enden Null.
Anders wird es, wenn du das Voltmeter draußen hast wo kein Magnetfeld ist. Du sitzt im Labor und aus Deiner Sicht bewegt sich die Schleife durch das Magnetfeld. Das ist nun ein komplett anderes Bezugssystem. In diesem ist das elektrische Feld im inneren des Stabes nicht Null sondern E=B*v, daher misst du nun am Voltmeter eine Spannung, und diese ist genau U = B*v*l
Alles eine Frage des Bezugssystems. Hier gelten die Gesetze der speziellen Relativitätstheorie. Nicht zuletzt heißt die Originalarbeit von Einstein aus dem Jahr 1905 „zur Elektrodynamik bewegter Körper“.
Der Weg von Klemme A zur Klemme B kann beliebig sein. Da man hier ein wirbelfreies elektrisches Feld hat (wir haben ja kein sich änderndes Magnetfeld) ist die Spannung von A nach B wegunabhängig und ein Voltmeter wird diese Spannung anzeigen (solange seine Strippen nicht in das Magnetfeld ragen und sich dort bewegen).
Die Spannung Uab ist aber da, egal ob da ein Voltmeter dranhängt oder nicht. Der Weg der Strippen ist hier auch völlig egal, du kannst auch einen Umweg von ein paar Metern machen um von A nach B zu kommen, du kannst auch ein 100m langes Kabel nehmen und auf einer Trommel aufwickeln – es ändert nichts daran, dass die Spannung immer gleich gemessen wird.
Mathematisch:
Im jedem wirbelfreien elektrischen Feld ist
∫ E ds = U unabhängig vom Weg.
Hast du diese Zeichnung selbst erstellt? Das E-Feld würde ich nicht einzeichnen; seine Wirkungsweise und Richtung stimmt zwar, aber es verwirrt höchstens.
Folgend ist eigentlich jeder Fall von Induktion sehr schon beschrieben und schrittweise hergeleitet: https://www.leifiphysik.de/elektrizitatslehre/elektromagnetische-induktion
Flächenänderung ist keine "Annahme", sondern eine Folge daraus, dass man die Spannung nicht am bewegten Stab-Ende abnehmen will und kann, sondern eben (wie in elektrischen Generatoren) irgendwo an einem fixen Anschluss.
Der Zusammenhang mit der so konstruierten Flächenänderung besteht bei jeder Leiterschleife, also sowohl für die gezeichnete, wie auch für Spulen mit mehreren Windungen.
Ja aber im Bild das ist ja keine richtige leiterschleife denn sie ist ja nicht geschlossen das hat mich verwirrt
Denn die Fläche des Leiters ändert sich ja prinzipiell nicht seine gesamte fläche ist durchgehend vom b Feld durchsetzt
Doch, sie ändert. Es geht nicht um die Fläche "des Leiters", sondern um die vom Leiter umschlossene Fläche. Und die nimmt natürlich zu, wenn der Stab nach rechts wandert, während die andern Teile an Ort bleiben.
Ja ich verstehe was du meinst aber müsste die Fläche nicht geschlossen sein und das ist sie ja links nicht. Und die Formel ist ja U=l*v*B
Das ist die gleich als wenn ich einen Leiter ohne metallschienen betrachte also macht es doch keinen Unterschied oder nicht?
https://pawn.physik.uni-wuerzburg.de/einfuehrung/SS06/23%20Induktion.pdf
Hier sind beide Beispiele nochmal angesprochen am Ende von Seite 4 und Anfang von Seite 5. worin besteht nun der unterschied beider Experimente, denn einmal wird über die Fläche berechnet und einmal über das gleichsetzen von F elektrisch und F lorentz. Und für N=1 sind die Formeln identisch
Ist das ein elektrisches Feld, das in Rot eingezeichnet ist, oder ein Magnetfeld?
Es wird höchstens ein Wirbelstrom induziert, falls das ein Zylinderförmiger Leiter (Draht) ist.
Falls es eine Platte ist, kommen die Elektronen exakt auch dich als Betrachter zu. Und zwar an jeder Stelle der Platte. Dies bedeutet, dass der technische Strom sich von dir wegbewegt, wie dies ja auch die Symbole im Hintergrund angezeigt ist.
Aber ganz schlau werde ich aus deiner Fragestellung noch nicht.
Oben und unten ist eine Schiene auf der der Leiter rollen kann. Er rollt von links nach rechts und das B Feld geht in den Bildschirm rein nun kann man die induzierte Spannung im Leiter bestimmen
jeder leiter hat doch n magnetfeld wenns durch strom durchflossen wird oder nicht?
Ja kann dir einigermaßen folgen aber Induktion wird ja zb durch flächenänderung hervorgerufen. Aber die Fläche in der Zeichnung ist ja nicht geschlossen man könnte die Schienen ja auch einfach weglassen und man hat nur Induktion durch Bewegung. Für beide Fälle gelten dieselben Formeln warum kann man hier dennoch über die Fläche gehen?