Hilfe bei Mathe Aufgabe?
Hallo,
die Aufgabe lautet:
Untersuchen Sie rechnerisch, ob es eine ganzrationale Funktion dritten Grades mit den folgenden Eigenschaften gibt. Falls möglich, geben Sie die Funktionsgleichung an und skizzieren Sie ihren Graphen.
c) Der Graph berührt die x-Achse an der Stelle x = 2 und hat einen Wendepunkt W(0|4).
stimmt es, dass es bei c) keine ganzrationale Funktion dritten Grades mit den angegeben Eigenschaften gibt? oder mach ich etwas falsch?
f(x)=ax^3+bx^2+cx+d
f’(x)=3ax^2+2bx+c
f”(x)= 6ax+2b
Es Ergeben sich die Gleichungen:
f(2)=0
f(0)=4
f”(0)=0
Wenn man das dann in die Ausgangsgleichung einsetzt, ergibt sich:
8a+4b+2c+d=0
d=4
2b=0
jetzt müsste ich die Gleichungen ja mit Einsetzungs/Gleichsetzungs/Additionsverfahren lösen, aber irgendwie weiß ich nicht wie…
3 Antworten
alles korrekt
8a+4b+2c+d=0 ;
d=4 ;
2b=0 = b ;
fehlt noch , wird häufig übersehen , f'(2) = 0 , weil ein Berührpunkt immer ein rel Max oder Min ist !
.
Also noch
0 = 12a + 4b + c dazu
.
Weil d und b schon bekannt sind , kannst du alles reduzieren zu
8a+4*0+2c+4=0
und
12a + 4*0 + c = 0
.
8a + 2c + 4 = 0
12a + c = 0 .........................c eleminieren mit dem Additionsverfahren
untere Glg mal -2
-24a - 2c = 0
addieren
-16a + 0 + 4 = 0
-16a = -4
.
Kontrolle Rechenmagd/knecht
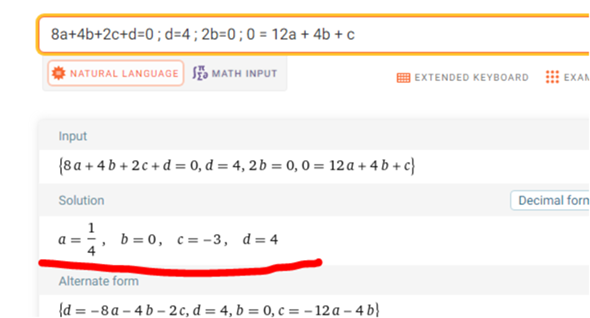
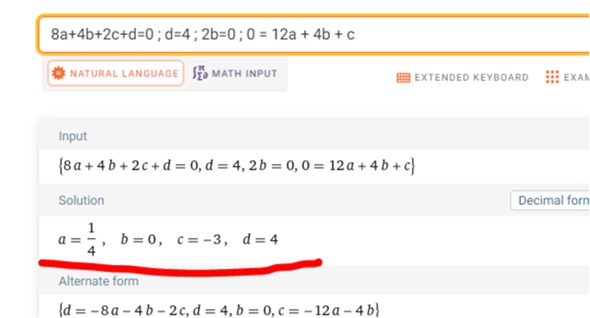
so sieht deine Fkt aus . Wunderschön :)))
f(x) = 0.25*x³ - 3x + 4
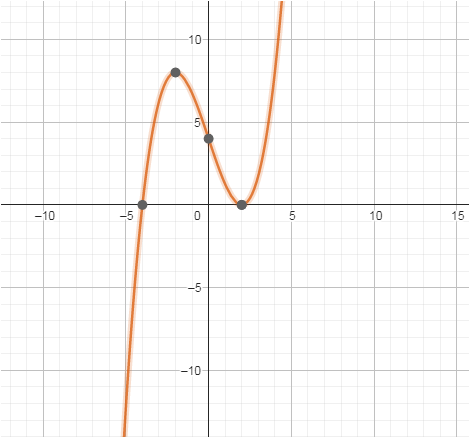
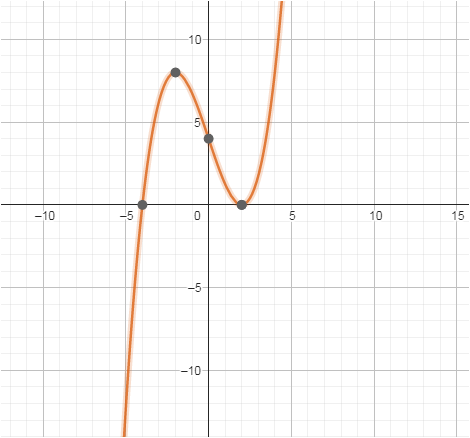
Deine Herangehensweise ist richtig, du hast jedoch eine wichtige Eigenschaft übersehen. Der Graph berührt die x-Achse an der Stelle x = 2, das bedeutet, dass die Funktion an diesem Punkt eine doppelte Nullstelle hat. Daher setzen wir die Ableitung der Funktion f(x) auf diesem Punkt gleich Null, d.h. f'(2) = 0.
Somit haben wir folgende Gleichungen:
1. f(2) = 0 (Da der Graph die x-Achse bei x = 2 schneidet)
2. f'(2) = 0 (Da der Graph die x-Achse bei x = 2 berührt)
3. f(0) = 4 (Da der Wendepunkt bei W(0|4) liegt)
4. f''(0) = 0 (Da bei einem Wendepunkt die zweite Ableitung gleich Null ist)
Die Gleichungen lauten also:
1. 8a + 4b + 2c + d = 0
2. 12a + 4b + c = 0
3. d = 4
4. 2b = 0
Für die vierte Gleichung folgt, dass b = 0 ist.
Setzen wir d = 4 und b = 0 in die erste Gleichung ein, erhalten wir 8a + 2c = -4.
Setzen wir b = 0 in die zweite Gleichung ein, erhalten wir 12a + c = 0.
Jetzt haben wir ein Gleichungssystem mit zwei Unbekannten, das wir lösen können:
12a + c = 0 => c = -12a
8a + 2c = -4 => 8a - 24a = -4 => -16a = -4 => a = 0.25
Setzen wir a = 0.25 in die Gleichung c = -12a ein, erhalten wir c = -3.
Die Funktionsgleichung lautet also: f(x) = 0.25x^3 + 4.
Bitte beachte, dass die Ableitungen f'(x) und f''(x) in diesem Fall nicht verwendet wurden, um die Konstanten a, b, c und d zu bestimmen. Sie wurden lediglich verwendet, um das Gleichungssystem aufzustellen.
c = -3.,,,,,,,,,,,,,,,,,,,,,,,,,,, das fehlt dann aber bei dir als -3x , oder ?
Dir fehlt eine Bedingung, wenn du vier unbekannte a,b,c,d hast. Diese lautet f'(2)=0, weil die x-Achse hier berührt wird.
f(x)=x SCHNEIDET die x-Achse. Ein BERÜHREN impliziert eine mindestens zweifache Nullstelle, so dass hier wenigstens die erste Ableitung Null ergibt. Vertrau mir.
Es ist aber nicht gesagt, dass dort die Funktion parallel zur x-Achse ist. f(x) = x berührt auch die x-Achse aber da ist f'(0) ≠ 0, Es sind nicht genügend Bedingungen gegeben um eine eindeutige Funktion zu erhalten. Daher gibt es unendlich viele.