Graphen mathematisch beschreiben?
Guten Abend, ich sitze gerade an meinen Hausaufgaben und komme nicht weiter. Die sieht wie folgt aus. Wir mussten bei einem Experiment einen Kondensator auf- und entladen. Dabei sollten wir die Spannung alle 10s messen. Haben wir auch gut hinbekommen. Und die Graphen sollten wir auch in ein Diagramm einzeichnen, geling uns auch ganz gut. Jetzt sollen wir aber "den Verlauf der Kurve mathematisch möglichst gernau erläutern" Wie mache ich das? :D
LG
4 Antworten
Der Graph ist in der Tat gelungen.
Eine Meßkurve in eine mathematische Funktion zu überführen, ist in der Praxis ein ständiges Problem. Dementsprechend gibt es dafür Dutzende von unterschiedlichen Methoden. Kann daher nur schildern, wie ich das Problem angehen würde.
Da überlege ich zuerst, um was für einen technischen Vorgang es sich handelt und ob es da schon passende Funktionen gibt. Man muss das Rad ja nicht jedesmal neu erfinden. Dann setze ich in diese Funktion die gemessenen Werte ein, um die fehlenden Parameter zu ermitteln.
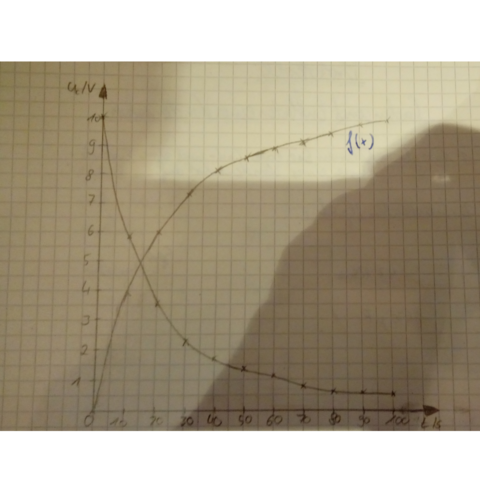
Zunächst gibt es mal zu überlegen, was praktisch passiert. Hier gibt es einen Potentialunterschied (Spannungsdifferenz), der sich ausgleicht. Ein bestimmter Wert kann dabei nicht überschritten werden, egal wie lange man t wählt. Solche Ausgleichsvorgänge nennt man beschränktes Wachstum. Das läuft immer in einer e-Funktion ab. Es fängt schnell an und nähert sich ganz langsam dem Maximalwert.
Die allgemeine Formel für das beschränkte Wachstum lautet (siehe auch wiki):
B(t) = S - (S - B0) * e^(k * t)
B ist die Bestandsgröße, also der y-Wert. Hier ist das die Spannung U
S ist der Grenzwert, hier beim Laden 10V, beim Entladen 0V
B0 ist der Anfangswert bei t = 0. Hier wäre es beim Laden 0 V und beim Entladen 10 V.
k ist die sogenannte Wachstumskonstante. Die gibt an, wie schnell ein Vorgang abläuft und die müssen wir rausfinden.
Ich beschränke mich auf die Ladekurve.
Es gilt also:
U(t) = 10 V - (10 V - 0 V) * e^(k * t)
U(t) = 10V - e^(k * t)
e^(k * t) = 10V - U(t)
k * t = ln(10 V - U(t) )
k = ln(10 V - U(t)) / t
So, und nun kann man die ermittelten Zahlenpaare einsetzen und für jeden Meßpunkt k ausrechnen. Am Ende bildet man das Mittel aller errechneten k, um die Streuungen auszugleichen, und hat dann die mathematische Funktion zum Graphen.
Das Ergebnis wäre dann:
Die mathematische Funktion zum Graphen lautet:
U(t) = 10V - e^(k * t)
Bei der Entladekurve geht das genauso.
Für fallendes Wachstum lautet die Formel:
B (t) = S + (B0 - s) * e^(k * t)
Soeben entdecke ich einen Rechenfehler, weil das von den Dimensionen nicht hinkommt, sorry.
U(t) = 10 V - (10 V - 0 V) * e^(k * t)
U(t) = 10 V - 10 V * e^(k * t)
U(t) = 10 V * (1 - e^(k * t) )
U(t) / 10V = 1 - e^(k * t)
e^(k * t) = 1 - U(t) / 10V
(k * t) = ln(1 - U(t) / 10V)
k = ln(1 - U(t) / 10V) / t
Sollt ihr versuchen, Funktionsgleichungen aufzustellen, oder nur allgemein beschreiben, wie die Graphen verlaufen?
Bei beiden Graphen habt ihr exponentielle Verläufe; bei f(x) ein beschränktes exponentielles Wachstum bis zu einem bestimmten Maximum; bei dem anderen eine exponentielle Abnahme.
Die unbeschriftete Funktion beginnt bei 10V und hat nach 10s noch ca. 5,8V, also nur noch 58% vom Startwert; als Funktionsgleichung:
g(x)=Startwert * Änderungsrate^Zeitperiode
g(x)=10 * 0,58^(1/10s)
Die Funktion f hat als Maximalwert die 10V und startet bei 0; nach 10s ist der Wert 4 erreicht:
f(x)=10 * (1-0,4^(1/10s))
(passen zwar beide nicht ganz zu den ermittelten Werten, aber in etwa hauts schon hin...)
Tipp: Es sind beides Exponentialfunktionen...
einmal beschränktes Wachstum nach oben und das andere Mal eine Hyperbel