Gegenüberliegende Winkel beim Parallelogramm gleich groß?
Hey Leute,
ich brauche ganz dringend Hilfe. Ich schreibe morgen eine Mathe Arbeit und muss dafür den Beweis dafür wissen, warum die gegenüberliegenden Winkel bei einem parallelogram gleich groß sind.
Ich habe schon mehrere Videos angeschaut aber finde nicht wirklich etwas dazu. Oder verstehe es nicht 🫤.
Außerdem habe ich so viele verschiedene Dinge dazu gehört. Man soll das parallelogram, durch eine gerade, in zwei Dreiecke einteilen und dann mit dem kongruent Satz “SSS” beweisen.
Oder
Man soll die Seiten erweitern mit Hilfslinien und so an die Sache dran gehen.
Aber ich weiß einfach nicht wie ich es jetzt machen soll.
Hat da jemand Ahnung von?
vielen vielen Dank!!
sophie :)
2 Antworten
sss

damit es ein Par ist , müssen die parallelen Seiten gleich lang (groß) sein
und BD ist in beiden Dreieck gleich
Daher ist ABD kongruent zu BDC
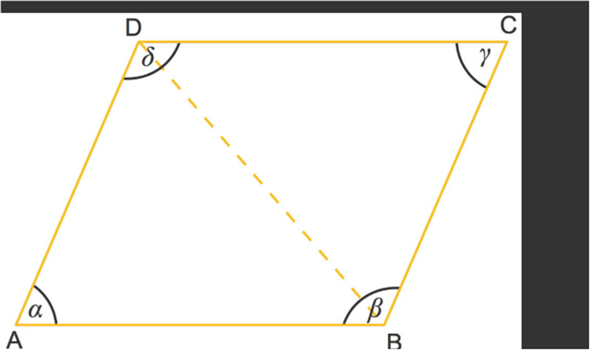
Stell dir ein Parallelogramm ABCD vor, bei dem AB ∥ CD und AD ∥ BC (gegenüberliegende Seiten sind parallel).
Jetzt kommt der Trick:
➤ Zeichne eine Diagonale von A nach C.Damit hast du zwei Dreiecke:
- 🔺 Dreieck ABC
- 🔺 Dreieck CDA
In beiden Dreiecken gilt:
- Seite AC ist gemeinsam
- AB = CD (weil gegenüberliegende Seiten im Parallelogramm gleich lang sind)
- AD = BC (ebenfalls gleich lang)
Du hast:
👉 Zwei Seiten und die eingeschlossene Seite gleich ⇒ SSS-Satz
Das heißt:
🔺 Dreieck ABC ≅ Dreieck CDA → sie sind kongruent
Fazit:Weil die Dreiecke kongruent sind, sind auch ihre Winkel gleich:
▶ Winkel D = Winkel B
▶ Winkel A = Winkel C
💡Wenn man ein Parallelogramm entlang einer Diagonalen teilt, entstehen zwei kongruente Dreiecke (SSS-Satz).
Daraus folgt: Gegenüberliegende Winkel sind gleich groß.