Funktion 4. Grades?
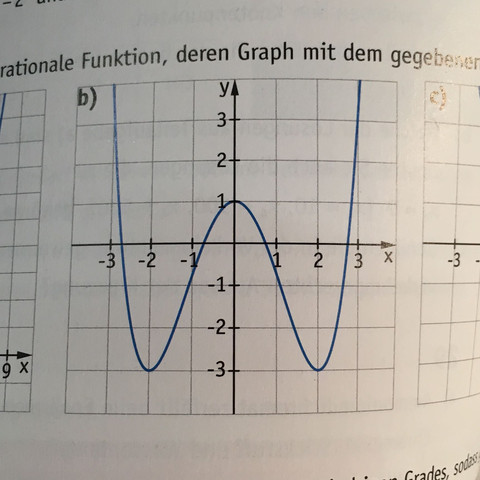
Hallo, ich suche zu diesem Graphen eine Funktion. Mir fehlt eine Bedingung, also falls jemand helfen könnte, wäre das sehr hilfreich.
Ich habe:
f'(0)= 0
f(0)= 1
f'(2)= 0
f(2)= -3
7 Antworten
achsensymmetrisch: f(x) = f(-x)
(-x)^(2n) = x^(2n), n ∈ IN
(-x)^4 = x^4 und (-x)^2 = x^2
f(x) = ax^4 + bx^2 + c
f'(x) = 4ax^3 + 2bx
f(0) = 1 = a * 0^4 + b * 0^2 + c <=> c = 1
f(x) = ax^4 + bx^2 + 1
-3 = a * 2^4 + b * 2^2 + 1 = 16a + 4b + 1
0 = 4a * 2^3 + 2b * 2 = 32a + 4b
16a + 4b + 1 = -3
32a + 4b = 0
16a - 32a + 4b - 4b + 1 = -3
-16a + 1 = -3 |-1
-16a = -4 |/(-16)
a = 1/4
32a + 4b = 0
32/4 + 4b = 0
4b = -8
b = -2
f(x) = 1/4 x^4 - 2x^2 + 1
http://m.wolframalpha.com/input/?i=plot+f%28x%29+%3D+1%2F4+x%5E4+-+2*x%5E2+%2B+1
Hier braucht man Spezialwissen,wie ich es habe.
f(x)=x⁴-a2*x² diese ist eine Funktion,wie man sie im Bild sieht,ein nach oben offenes "W".Dies ist aber noch um 1 nach oben verschoben.
Die Funktion im Bild hat somit die Form f(x)=a4*x⁴+a2*x²+ao
mit f(0)=1 ergibt sich ao=1
1.f(x)=a4*x⁴+a2*x²+1 abgeleitet
2. f´(x)=0= 4*a4*x³+2*a2*x
mit f(2)=-3 ergibt -3-1=a4*2⁴+a2*2² ergibt (aus f(x)=a4*x⁴+a2*x²+1)
1. 16*a4+4*a2=-4 hier 2⁴=16 und 2²=4
2. 4*2³*a4+2*2*a2=0 aus f´(2)=0
ergibt das "lineare Gleichungssystem" LGS
1. 16*a4+4*a2=-4
2. 32*a4+4*a2=0 Lösung mit meinen Graphikrechner (GTR,Casio)
a4=0,25 und a2=-2
gesuchte Funktion somit f(x)=0,25 *x⁴-2*x²+1
Probe : f(2)=0,25*2⁴-2*2²+1=-3 und mit x=0 ist f(0)=1
gern gescheh´n.
Symetrie zur y-Achse entsteht nur ,wenn die "Exponenten gerade" sind.
also n=4 und n=2
bei f(x)=x^4+x^3+x^2 hier ist keine Sysmetrie zur y-Achse möglich.
gib in deinen GTR folgende Funktionen ein
f(x)=x⁴+2*x² und f(x)=-1*x⁴-2*x² und f(x)=x⁴+2*x² und notiere dir das Ergebnis für deine Unterlagen.
auch f(x)=x⁴+x^2+ao oder f(x)=x⁴-x²-ao oder f(x)=-1*x⁴-x²-ao
also alle Vorzeichen ausprobieren
Hallo,
da die Funktion achsensymmetrisch zur y-Achse ist, ist sie nach dem Schema f(x)=ax^4+bx^2+c aufgebaut.
Du brauchst also nur drei Bedingungen.
f(0)=1, also c=1
f(2)=-3 und f'(2)=0
f(2) bedeutet:
16a+4b+1=-3
16a+4b+4=0
4a+b+1=0
b=-4a-1
f'(2)=0 bedeutet, da f'(x)=4ax^3+2bx:
32a+4b=0
Da b=-4a-1:
32a-16a-4=0
16a=4
a=1/4
b=-2
f(x)=(1/4)x^4-2x^2+1
Du kannst es auch gleich über die Nullstellen der Ableitung machen:
Da die Extrema bei x=-2; 0 und 2 liegen, gilt:
f'(x)=ax*(x-2)*(x+2)=ax*(x^2-4)=ax^3-4ax (denn (x-2)*(x+2)=(x²-4) nach der 3. binomischen Formel)
Durch Integration kommst Du auf f(x):
f(x)=(1/4)ax^4-2ax^2+1 (da f(0)=1)
Nun f(2) berechnen, um auf a zu kommen:
4a-8a+1=-3
4a=4
a=1
Daher:
f(x)=(1/4)x^4-2x^2+1
Herzliche Grüße,
Willy
Die Nullstellen des Graphen kannst Du natürlich nicht benutzen, weil es unmöglich ist, sie genau genug abzulesen.
Sie liegen übrigens bei ±√(4±2*√3), also bei
±2,732050808 und ±0,732050808
Die Achsensymmetrie zur y-Ache führt dazu, dass der Funktionsterm nur gerade Exponenten (4, 2 und 0) haben kann
Die Funktion ist achsensymmetrisch zur y-Achse, d.h. alle Parameter vor ungeraden Potenzen von x sind gleich 0.
Dankeschön!