Diese Dreiecke kongruent zueinander/ wie kann man nachweisen?
3 Antworten

Hey man sagt dass zwei Dreiecke kongruent sind, wenn sie Deckungsgleich sind. Natürlich könntest du jetzt messen und dann die Fläche berechnen und schauen ob die gleich ist, allerdings kann es sein dass es dann ungenau ist. Deshalb kannst du es nicht genau sagen. Für mich schaut es so aus als ob die Kongruent wären, aber Beweisen musst du es selber. Stell einfach die Flächeninhalte gegenüber. Ist zwar nicht genau. Aber dafür sollte es reichen. Wenn das eine Schätzaufgabe ist kann ich außerdem erkennen dass das Dreieck an der mittleren Linie zuerst gespiegelt, und dann am Kopf gestellt wurde. Mit rechnerischen Beweisen kommst du dann nicht weit, vorausgesetzt es gibt keine Angabe.
Habe gerade gesehen dass du noch die fehlende Angabe reingeschickt hast. Ja die Dreiecke sind eindeutig kongruent!
LG

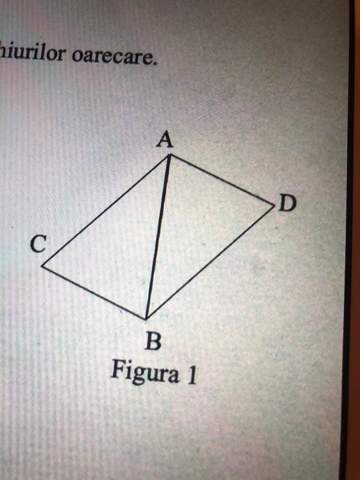
Soll das eine Fangfrage sein, oder fehlt da was?
So wie das abgebildet ist, kann man das nicht nachweisen/prüfen.
Zwei Winkel sollten gegeben und eine Seite sollten zum Beispiel gegeben sein.
Oder die Figur ist als Parallelogramm beschrieben. Und durch das Parallelogramm läuft Mittig die Diagonale, welche die zwei Dreiecke bildet.
Aber so, nur von dem Bild, kann man nicht mal sagen, dass das Dreiecke sind.
Gruß

Dann musst Du jetzt nachweisen, dass man unter den genannten Bedingungen nur deckungsgleiche Dreiecke konstruieren kann.
Evtl. geht ein Beweis durch Widerspruch? Du versuchst Dreiecke zu konstruieren, die nicht deckungsgleich sind.
Gruß

Kongruent heißt deckungsgleich und das sind sie.
Sie haben die gleichen Seitenlängen und Winkel.
In der Aufgabenstellung wird noch gesagt, dass: der Winkel ABC= Winkel BAD und dass die Seite BC kongruent zu der Seite AD ist