Definitionsbereich und Zielbereich einer bijektiven Funktion?

Hallo, ich soll zu folgender Funktionsgleichung:
f(x) := (x+2)(x-2)^-1
einen möglichst großen Definitionsbereich D ⊆ R und einen passenden Zielbereich Z ⊆ R geben, sodass f : D → Z dann eine bijektive Funktion ist.

Mein Ansatz ist:
D = R \ {2}
Z = R

In der Lösung steht allerdings für Z: Z = R \ {1}

Kann mir jemand erklären wie ich auf die 1 komme?

Answer 1

[evtldocha]

Vielleicht hilft die Skizze, um den Zielbereich zu erkennen:

Konkret müsstest Du das Globalverhalten der Funktion untersuchen. Zusammenfassend:

$\lim_{x\rightarrow\pm\infty}\frac{x+2}{x-2}=\lim_{x\rightarrow\pm\infty}\ \frac{1+\frac{2}{x}}{1-\frac{2}{x}}=+\ 1$

Comments

[tobi2859]

Ah okay, danke!

Answer 2

[Rhenane]

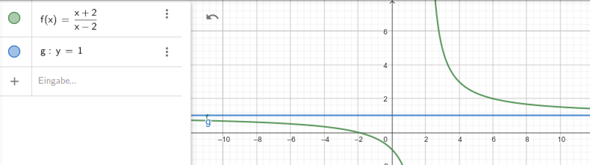
Diese gebrochen-rationale Funktion hat eine waagerechte Asymptote bei y=1. Setzt Du f(x)=1 stellst Du fest, dass diese Gleichung nicht "aufgeht", d. h. diese waagerechte Asymptote wird auch zwischendurch nirgendwo geschnitten; somit fällt y=1 aus der Wertemenge.