An welcher Stelle nimmt die Funktion den angegebenen Funktionswert an?
Hallo,
ich lerne hier gerade für meine Mathearbeit morgen, verstehe aber diese Aufgabe nicht.
Kann mir es vielleicht jemand erklären, und am besten ein Beispiel geben?
Das wäre nett.
Danke schon mal im Voraus :)

3 Antworten
Du weißt ja was Eine funktion ist und was dafür die allgemeine Formel ist oder?
y=mx+b
Dann musst du den Grafen für die erste Funktion zeichnen, also in diesem Fall ist bei a) x die Steigung also 1x deswegen geht die gerade in einem Winkel von 45° nach oben. Ich hoffe das habt ihr auch schon gelernt
Und dann musst du schauen an welcher Stelle von der gerade die Zahl 4 auf der y-Achse steht und dann mit dem Grafen schauen welchen Wert dann der y-Wert hat.
Wir machen das auch gerade und schreiben am Mittwoche auch eine KA darüber
Das mit dem ()² hatten wir noch nicht also kann ich dir da nicht helfen
Viel Glück bei der Arbeit
Du musst für y den gegebenen Funktionswert einsetzen und die quadratische Gleichung in x dann nach x auflösen. Hier am Beispiel (a):
4 = (x + 4,5)^2
0 = (x + 4,5)^2 - 2^2
(x + 4,5 - 2) * (x + 4,5 + 2) = 0
(x + 2,5) * (x + 6,5) = 0
x = - 2,5 v x = -6,5
Ich habe hier die 3. Binomische Formel angewandt, weil sich in diesem Fall das Ergebnis leicht ablesen lässt. In allen anderen Fällen musst Du die quadratische Gleichung mittels pq-Formel lösen…
Hey wir benutzen momentan in dem Thema nur die pq-Formel..
Irgendwie habe ich nichts bei deiner Rechnung verstanden 😅
Also wenn ich jetzt meinen Graphen für beispielsweise b) gezeichnet habe, wie finde ich dann heraus an welcher Stelle die Funktion jetzt den Funktionswert annimmt?
Einfach eine Parallele zur x-Achse zeichnen, die die y-Achse beim angegebenen Funktionswert schneidet (bei Aufgabe (a) also bei y = 4); die x-Koordinaten der Schnittpunkte dieser Parallelen mit dem Graphen sind gerade die gesuchten Lösungen…

Erst wenn man den SP kennt , weiß man wo die Parabel liebt
nun schauen wo y = -7 ( es sind zwei Punkte )
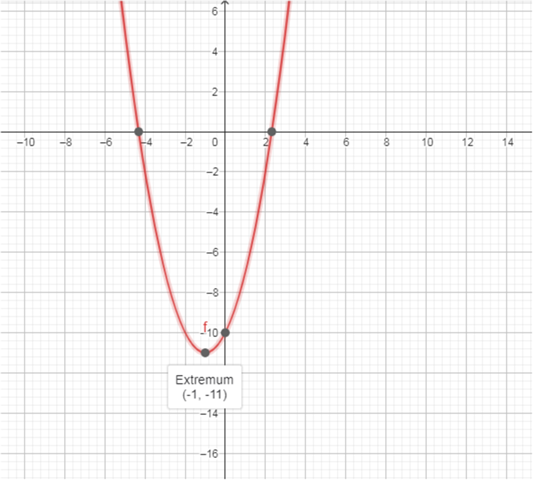
Uff nein das ist leider falsch. Es handelt sich hier nicht um geradengleichungen sondern um Parabeln.