Zylinder-artigen Volumen berechnen (Integration)?
Hallo, alle! Es gäbe da eine Matheaufgabe, die ich nicht lösen kann. Könnte mir jemand bitte dabei helfen? Sie lautet folgendermaßen:
"Es gibt einen geraden Zylinder mit einer Höhe von 5, dessen Grundfläche, die sich in der Ebene Oxy befindet, von der Achse Oy sowie der Halbellipse x = 5/2 * sqrt(16-y^2) begrenzt ist. Man schneidet den Zylinder mithilfe einer schiefen Ebene, dessen Gleichung x = 2z ist. Aufgabe: Rechnet den Volumen der Zylinder-ähnlichen-Figur, die durch die Ebene der Grundfläche sowie der schrägen Ebene (x = 2z) begrenzt wird (siehe Bild)".
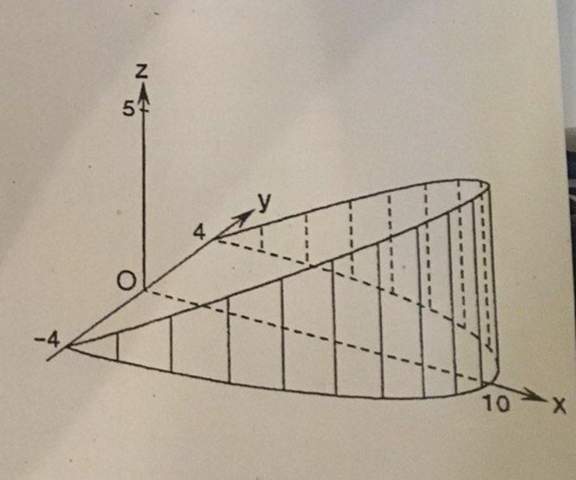
Für diese Aufgabe werde ich sehr wahrscheinlich Integralen benutzen werden, doch ich weiß nicht wie. Könnte mir jemand bitte dabei helfen, das/die Integral(en) zu finden, das/die diesen Volumen ausrechnen kann/können?
Vielen Dank im Voraus
2 Antworten
Hallo,
das läßt sich über ein Doppelintegral (auch Flächenintegral genannt) berechnen.
Dazu solltest Du aber zunächst einmal die Funktionsgleichungen nach z bzw. auflösen.
Aus x=2z folgt z=x/2.
Das ist eine Flächenfunktion, die den oberen Deckel des Körpers bildet, dessen Volumen Du berechnen möchtest.
Den unteren Deckel bildet eine Fläche in der xy-Ebene, die durch zwei Halbellipsen begrenzt ist.
Da das Ganze symmetrisch zur x-Achse ist, betrachtest Du bei Deinen Berechnungen nur den Bereich oberhalb der x-Achse. Zum Schluß brauchst Du Dein Ergebnis nur noch zu verdoppeln.
Du berechnest nacheinander zwei Integrale.
Das erste Integral ist das der Flächenfunktion z=x/2.
Da Du nur den Bereich oberhalb der x-Achse betrachtest, bildet diese die Untergrenze. Die Obergrenze in y-Richtung ist die gegebene Wurzelfunktion, die nach Auflösung nach y so lautet: y=2*Wurzel (4-x²/25).
Du integrierst z=x/2 nach y und setzt als Obergrenze die nach y umgestellte Halbellipsenfunktion ein, als Untergrenze einfach 0.
Wenn Du x/2 nach y integrierst, wird x/2 wie ein konstanter Faktor betrachtet.
Die Stammfunktion von f(x;y)=x/2 lautet demnach (x/2)*y, wenn nach y integriert wird (die Integrationskonstante C schenke ich mir; die spielt bei dieser Berechnung keine Rolle).
Für y setzt Du nun die Funktion 2*Wurzel (4-x²/25) ein und ziehst davon das ab, was Du erhältst, wenn Du für y eine Null einsetzt, also Null.
Als Ergebnis der Integration der Flächenfunktion nach y bekommst Du daher
(x/2)*y=(x/2)*2Wurzel (4-x²/25)=x*Wurzel (4-x²/25).
Nun hast Du eine Funktion bekommen, die nur noch von x abhängig ist.
Diese integrierst Du nun nach x in den Grenzen von 0 bis 10.
Die Stammfunktion findest Du über die Substitution u=x²/25.
Das Ergebnis (66 2/3) multiplizierst Du noch mit 2, weil Du ja nur den halben Körper (den Teil oberhalb der x-Achse) berechnet hast.
Herzliche Grüße,
Willy
Die Flächenfunktion f(x;y), die hier z=x/2 lautet, bildet den 'Deckel' eines prismen- oder zylinderartigen Körpers, dessen Grundfläche in der xy-Ebene in der Regel von zwei Funktionen und zwei Parallelen zur y-Achse begrenzt wird.
Hier hast Du als Grundfläche eine Halbellipse, von der ich nur den oberen Teil berechnet habe. Die Grenzen in y-Richtung lauten 0 und f(x), die Grenzen in x-Richtung lauten 0 und 10.
Wenn Du senkrecht darüber einen Deckel in der Höhe z befestigen würdest, bekämst Du einen Körper, dessen Volumen Du einfach nach der Formel Grundfläche mal Höhe berechnen könntest. Das ginge mit einem einfachen Integral für die Ellipsenfunktion.
Hier aber hast Du es mit unterschiedlichen Höhen zu tun und kannst die Sache nicht mit einer einfachen Multiplikation lösen. Du machst also etwas anderes:
Du teilst die Grundfläche in Rechtecke auf. Eins dieser Rechtecke könnte etwa zwischen x=2 und x=3 liegen sowie zwischen y=1 und y=2. Die Ecken wären dann von links unten über rechts oben nach links oben (2|1); (3;1); (3|2) und (2|2). Nun errichtest Du über diesem Rechteck senkrechte Wände, die jeweils bis an die Deckfläche stoßen, die in diesem Fall eine Schräge ist, die am linken Rand die Höhe 0 und am rechten Rand die Höhe 5 hat. Die Höhe beträgt dabei jeweils 1/2 x. Die linke Wand des Rechtecks wäre demnach eine Einheit hoch (2/2), der rechte Rand wäre 1,5 (3/2) Einheiten hoch. In y-Richtung würde sich die Höhe nicht verändern.
Um das Volumen der Säule zu berechnen, könntest Du näherungsweise 1,25, also den Mittelwert zwischen 1 und 1,5 als Höhe nehmen und bekämst als Näherung für das Volumen der Säule 1,25 Kubikeinheiten heraus.
Wenn Du das mit der gesamten Fläche machst, sie also lückenlos in kleine Rechtecke einteilst, die jeweiligen Volumina näherungsweise berechnest und alle Volumina anschließend addierst, bekommst Du eine Näherung an das Gesamtvolumen des Körpers. Es sollte klar sein, daß die Näherung um so genauer wird, je kleiner und zahlreicher die Rechtecke mit ihren Quadern darüber sind. Sind die Rechtecke unendlich klein und unendlich zahlreich, hast Du den Grenzwert, der dem tatsächlichen Volumen entspricht.
Genau das tut das Doppelintegral. Mit dem inneren Integral, das gewöhnlich nach y erfolgt und das sich auf die Funktion der Deckschicht bezieht, teilst Du die Grundfläche in unendlich viele Streifen mit der Dicke dx auf. Da jeder Streifen unendlich dünn ist, spielt die Höhendifferenz in x-Richtung keine Rolle. Die Höhe verändert sich nur noch in y-Richtung. Wenn Du also die unterschiedlichen Höhen, die so ein dünner Streifen in y-Richtung aufweist, in unendlich viele unendlich schmale Abschnitte einteilst, die jeweils die Höhe dy haben und deren einzelne Höhenwerte aufaddierst, bekommst Du den exakten Mittelwert aller unterschiedlichen Höhen dieses Streifens und kannst so sein genaues Volumen berechnen. Dabei ist die Untergrenze die Funktion (hier: y=0), die die Fläche nach unten hin abschließt, und als Obergrenze die Funktion (hier:
y=2Wurzel (4-x²/25), die die Fläche nach oben hin abschließt. Jeder einzelne Streifen hat, da hier die Untergrenze immer gleich Null ist (x-Achse), den jeweiligen FunKtionswert der Ellipsenfunktion als Höhe in y-Richtung.
Die Höhe in z-Richtung, die als Mittelwert für den kompletten Streifen genommen werden kann, bekommst Du, wenn Du f(x;y), also die Funktion des Deckels, nach y integrierst.
Wenn Du das getan hast, brauchst Du nur noch die einzelnen Volumina der unendlich dünnen und unendlich vielen Streifen von x=0 bis x=10 zu integrieren, um das Gesamtvolumen des Körpers zu erhalten.
Das innere Integral liefert Dir also eine Funktion für das Volumen einer einzelnen Scheibe, das äußere summiert die Volumina der einzelnen Scheiben, die von links nach rechts aneinandergelegt werden, bis sie den Körper völlig ausfüllen, auf und liefert so das Gesamtvolumen.
Wenn Du bei einem Doppelintegral die Höhe überall auf 1 setzt, kannst Du mit seiner Hilfe auch Flächen zwischen Funktionen ausrechnen, denn Bei einer Höhe 1 sind die Maßzahlen für Grundfläche und Volumen logischerweise identisch. Läuft dann aber auf das Gleiche hinaus, als würdest Du einfach die untere Funktion von der oberen abziehen (eventuelle Schnittpunkte berücksichtigen und notfalls abschnittsweise integrieren!) und die Differenzfunktion integrieren.
Das Volumen von Prismen (2 parallele, deckungsgleiche Grundflächen) ist Grundfläche×Höhe.
Du hast eine zylinder-ähnliche Figur, damit also auch eine prismen-ähnliche Figur, daher gilt obige Formel.
Die Schnittebene geht von links unten nach rechts oben → sie halbiert also deinen Körper!
Fläche für Ellipse = a·b·𝜋
Die Formel für deinen Zylinder ist also:
V = a·b·𝜋·h/2 = 10·4·5·𝜋/2 = 100𝜋.
Du kannst die Lösung natürlich auch mit Integral herbeiführen (frag mich jetzt nicht, wie - ich weiß es nicht!), aber warum umstänlich, wenn es einfach geht? ;-)
Vielen, vielen Dank für die ausführliche Antwort! Das hat sicher viel Mühe oder Zeit gekostet. Rechnerisch gesehen, verstehe ich alles, doch ich hätte noch eine kurze Frage. Könnte ich mir diese Rechnung folgendermaßen erklären? “Im Großen und Ganzen dient das integral von 0 bis y=2*Wurzel (4-x²/25) dazu die Fläche der Ellipse auszurechnen und z=x/2 ist die veränderliche Höhe”. Wäre diese Interpretation richtig?