Zentripetalkraft Aufgabe?
Hallo,
ich habe eine Frage zur folgenden zwei Aufgabe:
1) Ein Schnellzug durchfährt mit der Geschwindigkeit v=120 km/h eine Kurve vom Radius r=2500 m. Wie groß muss man die Überhöhung ü (in mm) der äußeren Schiene (Spurweite w=1435 mm) wählen, damit beide Schienen gleich belastet werden?
Theoretisch muss man ja schauen, dass die resultierende Kraft FR genau zwischen beiden Schienen ist, jedoch weiß ich gerade nicht so ganz wie man das mathematisieren kann.
2) Ein Körper (m=0,1kg) wird an einer Schnur (l=0,5m) auf einem Kreis, dessen Ebene senkrecht zur Erdoberfläche steht, herumgeschleudert.
a) Wie groß müssen mindestens die Winkelgeschwindigkeit und die Drehzahl pro Minute sein, damit der Körper im oberen Punkt seiner Bahn nicht herunterfällt?
b) Welche Reißfestigkeit (in N) muss die Schnur besitzen?
Hierbei möchte ich die Aufgabe zunächst bildlich verstehen: Wie stellt man sich das vor, kreist jetzt einfach ein Körper über einer bestimmten Stelle senkrecht zur Erdoberfläche im Kreis? Wieso, beziehungsweise was bestimmt, ob der Körper runterfällt und wieso?
Ich danke.
3 Antworten
Theoretisch muss man ja schauen, dass die resultierende Kraft FR genau zwischen beiden Schienen ist,
Ja - und da man davon ausgeht, dass der Schwerpunkt des Zuges mittig liegt, muss man nur schauen, dass die Richtung der Kraft (also Gewichtskraft plus Zentrifugalkraft (=Gegenkraft zur Zentripetalkraft)) senkrecht zur Gleisebene steht.
Zur 1. Aufgabe: Betrachtet man die Situation in einem mitrotierenden Bezugssystem, müssen sich die Kräfte auf den Zug zu null addieren.
(F_Z=Zentrifugalkraft).
Nun kann man eine Zerlegung in Komponenten machen, etweder horizontal/vertikal oder parallel/senkrecht zur Ebene, in welcher die Schienen liegen. Allenfalls Skizze machen.
Horizontal:
Vertikal:
Nun kann man z.B. die Gleichungen durcheinander dividieren und nach tan(alpha) auflösen. Damit lässt sich auch die Frage nach der Überhöhung beantworten.

Noch ergänzend: betrachtet man die Situation in einem Inertialsystem, tritt die Zentrifugalkraft nicht auf. In einem solchen Bezugssystem wird der Zug aber mit der Zentripetalbeschleunigung a_Z=v^2/r zum Mittelpunkt der Kreisbahn beschleunigt. Die erste obige Gleichung wird damit
Zur 2. Aufgabe: Ja, der Körper wird vertikal herumgeschleudert (Drehachse horizontal). Zu a): Im Grenzfall, wo der Körper gerade nicht herunterfällt, wird die Seilkraft im höchsten Punkt gleich null. Versuche, eine Gleichung für den obersten Punkt aufzustellen:
Auf der rechten Seite kommen die Kräfte hin, die auf den Körper wirken. Zu b): Betrachte dafür den untersten Punkt -dort ist die Seilkraft maximal- und stelle dafür eine Gleichung auf.
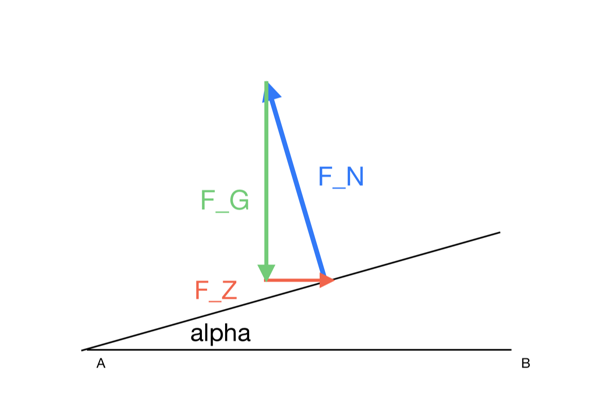
Ich habe oben eine einfache Skizze hinzugefügt.
Zur Division der Gleichungen: der Einwand ist berechtigt, da muss man grundsätzlich vorsichtig sein. Man kann hier die Terme mit der Normalkraft jeweils auf die rechte Seite bringen, und beide Gleichungen sind dann sicher ungleich null. Alternativ kann man eine Gleichung nach F_N auflösen und den Ausdruck dann in der anderen Gleichung einsetzen.
Im untersten Punkt wirkt dann die Gewichts und Zentrifugalkraft, oder?
Im untersten Punkt wirkt die Gewichtskraft nach unten und die (zu bestimmende) Seilkraft nach oben. Da die Zentripetalbeschleunigung gleich v^2/r ist (ebenfalls nach oben), muss gelten
m*v^2/r = F_S - m*g
Und jetzt bezogen auf den obersten Punkt? Da wirkt ja die Gewichtskraft nach unten und Zentripetalkraft ja eigentlich auch wobei ja eigentlich nicht. Ich verstehe golgendes logisch nicht so ganz: die Zentripetalkraft wirkt unten hoch, trotzdem wenn wir ganz oben sind, bleiben wir ja oben, wegen der scheinbaren Zentrifugalkraft, wieso wirlt diese Zentrifugalkraft dann auch unzen nicht runter?
Zur ersten Frage: Am obersten Punkt muss eine Zentripetalkraft wirken, sonst würde der Körper nicht auf der Kreisbahn bleiben, sondern geradeaus (bzw. im freien Fall) weiterfliegen.
Im Grenzfall, wo die Geschwindigkeit gerade noch genügt, dass der Körper im höchsten Punkt auf der Kreisbahn bleibt, ist die Seilkraft am höchsten Punkt gleich null. Die Zentripetalkraft m*v^2/r (die ja im Prinzip keine eigenständige Kraft ist wie die Gravitationskraft oder eine Seilkraft) entspricht dann gerade der Gewichtskraft.
In einem Inertialsystem erfolgt am höchsten Punkt eine Beschleunigung nach unten (Zentripetalbeschleunigung v^2/r), weshalb auch die resultierende Kraft -im Grenzfall gerade die Gewichtskraft- nach unten zeigen muss.
Eine Zentrifugalkraft tritt erst auf, wenn man die Situation im mitrotierenden Bezugssystem betrachtet. Das ist hier auf den ersten Blick etwas ungewohnt, das Bezugssystem dreht sich dann mit dem Seil und dem Körper mit. In diesem Bezugssystem ist der Körper in Ruhe, d.h. die resultierende Kraft muss gleich null sein. Am obersten Punkt wirken dann die Gewichtskraft nach unten, die Zentrifugalkraft mit gleichem Betrag nach oben.
Im mitrotierenden Bezugssystem am untersten Punkt: Körper ist wieder in Ruhe. Zentrifugalkraft wirkt nach unten, Gewichtskraft ebenfalls. Die Seilkraft wirkt nach oben und muss die ersten beiden Kräfte aufheben:
F_S - F_G - F_Z = 0
Für die Seilkraft gilt also am tiefsten Punkt
F_S = m*g + m*v^2/r = m*g + m*r*omega^2
Diese Gleichung gilt allgemein, nicht nur für den Fall, wo omega gleich der in a) gesuchten minimalen Winkelgeschwindigkeit ist.
Ich denke, ich habe es fast verstanden, danke dir schon Mal dafür. Die Zentripetalkraft muss quasi immer die Kraft sein, die die Kreisbewegung zustande bringt. Zum Seilbeispiel: Du hast hierbei zwischen zwei Bezugssystemen unterschieden. Aber es ist ja eigentlich so, dass es nur 1 maximal Kraft geben kann, die das Seil am Grenzfall haben muss. Ganz oben, wirkt die Gewichtskraft nach unten und die Zentripetal bzw Fugalkraft (die Kraft die die Kreisbewegung ermöglicht) nach oben. (Sie muss nach oben wirken und die Gewichtskraft kompensieren). Ganz unten finde ich es schwer: Die Gewichtskraft wirkt rutner, klar. Die Zentrifugalkraft so gibt es ja nicht, Die Zentripetalkraft, die die Kreisbewegung ermöglicht, muss entweder der Gewichtskraft entgegenwirken ( auf einem hohen Drehrrad beispielsweise) oder gleich 0 sein (die Normalkraft würde die Gewichtskraft kompensieren).
Was ist mein Denkfehler?
PS: Die Zentripetalkraft ist ja in diesem Sinne die "Zufkraft" des Seils, wenn man so will.
bin immernoch diesbezüglich am überlegen und wäre über eine weitere Antwort sehr erfreut :)
Die Zentripetalkraft muss quasi immer die Kraft sein, die die Kreisbewegung zustande bringt.
Ja, das kann man so sagen.
Aber es ist ja eigentlich so, dass es nur 1 maximal Kraft geben kann, die das Seil am Grenzfall haben muss.
Ja, eine Seilkraft -wie jede andere Kraft, die auf Wechselwirkungen mit einem anderen Körper zurückgeführt werden kann- ist nicht abhängig vom Bezugssystem.
Ganz oben, wirkt die Gewichtskraft nach unten und die Zentripetal bzw Fugalkraft (die Kraft die die Kreisbewegung ermöglicht) nach oben.
Noch einmal ausführlich das Beispiel mit dem vertikal an einem Seil rotierenden Körper.
Oberster Punkt in einem Inertialsystem: Allgemein wirken am obersten Punkt die Gewichtskraft und die Seilkraft nach unten. In einem Inertialsystem gibt es keine weiteren Kräfte! Die Zentripetalkraft ist keine eigenständige Kraft: die Gewichtskraft und die Seilkraft (bzw. im Grenzfall minimaler Winkelgeschwindigkeit die Gewichtskraft alleine) bilden im vorliegenden Fall gerade die Zentripetalkraft.
Wir wissen: Da der Körper sich auf einer Kreisbahn bewegt, muss die (Zentripetal-)Beschleunigung gleich v^2/r sein. Folglich gilt (m*a=F):
m*a = m*v^2/r = m*g + F_S
Je grösser die Winkelgeschwindigkeit, umso grösser die Seilkraft, das muss ja auch intuitiv so sein.
Im Grenzfall, wo die Winkelgeschwindigkeit gerade so gross ist, dass die Seilkraft verschwindet, gilt
m*v^2/r = m*g
Es wirkt dann am obersten Punkt nur noch die Gewichtskraft auf den Körper.
Oberster Punkt in einem mitrotierenden Bezugssystem: In einem solchen Bezugssystem ist der Körper in Ruhe, es muss also ein Kräftegleichgewicht vorliegen. Es wirkt eine Zentrifugalkraft m*v^2/r radial nach aussen bzw. oben, die Gewichtskraft und Seilkraft nach unten. Es gilt
0 = m*v^2/r - m*g - F_S
äquivalent zur Gleichung in einem Inertialsystem
Im Grenzfall gilt minmaler Winkelgeschwindigkeit gilt
0 = m*v^2/r - m*g
Die Zenrifugalkraft und die Gewichtskraft sind dann entgegengesetzt gleich gross.
Unterster Punkt in einem Inertialsystem: es wirken Gewichtskraft nach unten, Seilkraft nach oben. Die Zentripetalbeschleunigung beträgt v^2/r, es gilt also
m*v^2/r = F_S - m*g
Für die Seilkraft gilt somit
F_S = m*v^2/r + m*g
Unterster Punkt in einem mitrotierenden Bezugssystem: Gewichtskraft nach unten, Zentrifugalkraft nach unten, Seilkraft nach oben. Die Kräfte müssen sich zu null addieren:
0 = F_S - m*g - m*v^2/r
Dies führt wiederum auf die gleiche Seilkraft wie in einem Inertialsystem.
Hey, schöne Erklärung. Nur frage ich mich zurzeit folgendes: Die Zentripetalkraft ist ja im obersten Punkt quasi die Gewichtskraft und die Seilkraft (was die Zentripetalkraft ist, da jedoch w näherungsweise 0 ist, folgt für diese Kraft 0) -> Die Zentripetalkraft wird also folglich von der Gewichtskraft gebildet. Zwei Fragen: wieso wird die Zugkraft durch die Zentripetalkraft in diesem Sinne modeliert und zweite Frage, gibt es wirklich diesen Grenzpunkt mit w = 0? Die dritte Frage ist etwas abstrakt: wieso fällt der Körper am obersten Punkt nicht durch, also, ja er hat eine Bahngeschwindigkeit und der Richtungsvektor ändert sich ständig (es muss also eine Zentripetalkraft geben). Man könnte ja mit der Trägheit argumentieren, aber im obersten Punkt wirkt ja nur FG nach unten. Irgendwie eine schwere Frage.
Die Zentripetalkraft ist ja im obersten Punkt quasi die Gewichtskraft und die Seilkraft (was die Zentripetalkraft ist, da jedoch w näherungsweise 0 ist, folgt für diese Kraft 0) -> Die Zentripetalkraft wird also folglich von der Gewichtskraft gebildet.
Ja, im Grenzfall, wo die Winkelgeschwindigkeit gerade noch genügend hoch ist, sodass der Körper am höchsten Punkt nicht die Kreisbahn verlässt und herunterfällt, wird die Seilkraft im obersten Punkt gleich null und für Zentripetalkraft ist alleine die Gewichtskraft verantwortlich.
Die Winkelgeschwindigkeit ist deshalb aber nicht gleich oder annähernd gleich null:
Es gilt ja am obersten Punkt
m*r*omega^2 = m*g
d.h. im Grenzfall gilt für die Winkelgeschwindigkeit
omega=Wurzel(g/r)
wieso fällt der Körper am obersten Punkt nicht durch, also, ja er hat eine Bahngeschwindigkeit und der Richtungsvektor ändert sich ständig (es muss also eine Zentripetalkraft geben). Man könnte ja mit der Trägheit argumentieren, aber im obersten Punkt wirkt ja nur FG nach unten. Irgendwie eine schwere Frage.
Diese Frage verstehe ich nicht ganz. Ja, der Geschwindigkeitsvektor ändert sich laufend. Bei konstanter Winkelgeschwindigkeit (was mit einem Seil nicht erreichbar wäre), bleibt der Geschwindigkeitsvektor betragsmässig konstant und ändert nur die Richtung.
A1 Die Normalkraft auf die Gleise muss senkrecht auf die Gleisebene wirken. Mache eine Skizze und trage die Kraftpfeile ein.
Ich verstehe diesen Weg nicht zu 100%; wie bist du auf genau diese zerlegung gekommen (also ja die macht ja sinn, aber wie bist du darauf gekommen, dass es jeweils so formuliert sein muss)
2. Wenn ich die Gleichungen durcheinander dividiere, würde ich nicht 0/0 teilen?