3 Antworten
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Schule, Mathematik
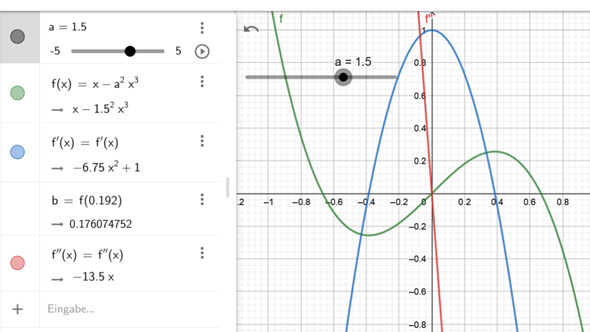
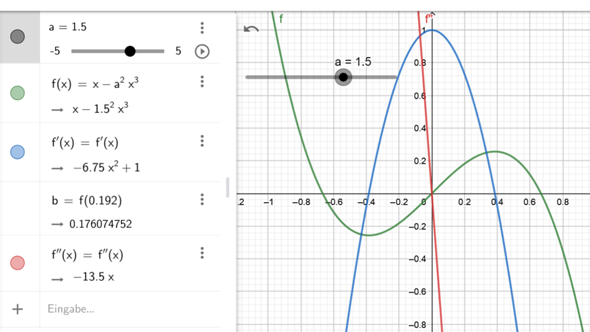
f(x) = x - a² * x³
f'(x) = 1-3a²x²
f'(x) = 0 = 1-3a²x²
3a²x² = 1
x² = 1/(3a²)
x1 = -1/(Wurzel(3)*a) und x2 = 1/(Wurzel(3)*a) mit a ungleich 0
An diesen Stellen gibt es Extremwerte.
f''(x) = 0 = -6a²x
Hieraus erkennt man, dass ein Faktor "-6a²" multipliziert mit x soll Null ergeben, dass x = 0 sein muss. Alle Wendestellen sind stets bei x = 0.
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Schule, Mathematik
f(x) = x - a² * x³
f'(x) = 1 - 3a² x²
NS: x - a²x³ = 0 | x ausklammern
x(1 - a²x²)= 0 | 3. Binom. Gesetz
x(1 - ax)(1+ax) = 0 |Satz v.Nullprodukt
gar nicht nötig
1.Fall: x₁ = 0
2.Fall: 1 - a²x² = 0
a²x² = 1
x² = 1/a²
x₂ = 1/a und a ≠ 0
gilt immer
3. Fall analog: x₃ = -1/a
Minimax: 1 - 3a² x² = 0
3a²x² = 1
x² = 1/(3a²)
x₁ = 1/(a√3)
x₂ = -1/(a√3)
y aus f(x) holen
f'' auf gleiche Weise. Sind noch Fragen?
Lass dich durch a nicht verblüffen, es
ist eine normale Zahl, die evtl. bei einer
Kurvenschar später belegt wird.
Woher ich das weiß:eigene Erfahrung – Unterricht - ohne Schulbetrieb
Nutzer, der sehr aktiv auf gutefrage ist
Schreib die Funktion doch mal mit Klammern hin.