Wo gibt es Fehler in meiner Vorgehensweise?

Ich gehe davon aus, dass der kleinste Wert sich auf den kleinsten Funktionswert bezieht. Gleichzeitig würde ich versuchen von Normalform zu Scheitelpunktform mit quadrat. Ergänzung zu gelangen und dann für f(x) 1 einsetzen. Dann gelange ich zu:

1 = (x-3)^2 - 9 + c

An diesem Punkt hatte ich überlegt, den X-Wert für die Scheitelpunktform aus der Ursprungsgleichung zu ermitteln mit - (2b/a) und dann in 1 = (x-3)^2 - 9 + c diesen X-Wert einzusetzen, aber dann komme ich auf x= 12 und wenn ich alles einsetze bei c auf -72 und das erscheint mir falsch zu sein.

Answer 1

[evtldocha]

Das mit der Scheitelpunktform ist ja schon mal der richtige Ansatz:

$f\left(x\right)=\left(x-3\right)^2-9\ +\ c$

Das heißt: Der Scheitelpunkt ist bei x = 3; y = - 9 + c, oder als Punkt geschrieben:
S( 3 | -9 + c). Da der Scheitelpunkt einer nach oben offenen Parabel auch der tiefste Punkt ist, muss gelten:

$-9\ +c\ =\ 1\ \ \ \ \ \ |\ +9$ $c=10$

Skizze:

Comments

[fagussylvatica]

So einfach? Ich dachte, es müsste dabei mehr gerechnet werden.

[evtldocha]

@fagussylvatica

So einfach - ja.

[evtldocha]

@fagussylvatica

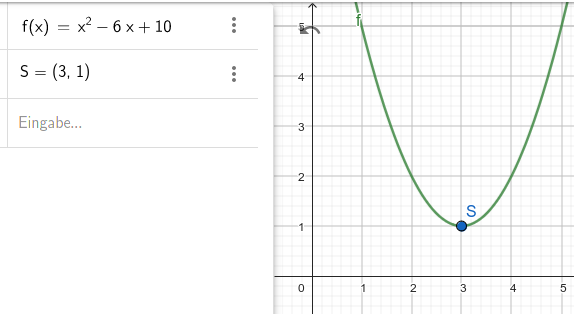
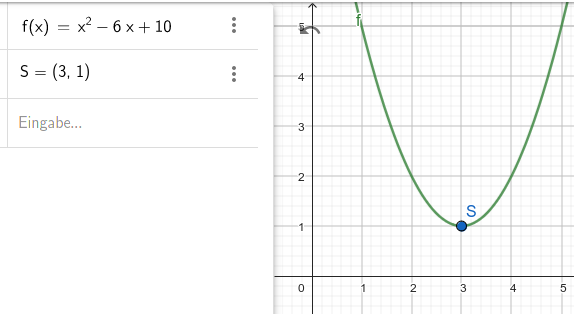
Nur zur Ergänzung:

Mit Deinem Ansatz hättest Du nach der Aufstellung der Scheitelpunktform f(3) = 1 rechnen müssen - was am Ende auf dasselbe hinausläuft.

[fagussylvatica]

@evtldocha

Okay, dann funktioniert die Formel zur Bestimmung von x in der Scheitelpunktform x = - (2b/a) wohl nicht.

[fagussylvatica]

@fagussylvatica

Ich habe meinen Fehler gefunden - Danke!

[fagussylvatica]

@fagussylvatica

Das was ich hier geschrieben habe ist großer Mist