Wieso stimmt die Ableitung vom logistischen Wachstum nicht?
Bevor sich irgendwer beschwert, Nein, ihr erledigt hier nicht meine Hausaufgaben, und nein, ich bin auch nicht zu faul zum recherchieren. Ich hab mich jetzt seit 2h damit beschäftigt aber komme zu keiner gescheiten Lösung.
Ich habe für logistisches Wachstum den Term
f(x)=1920/(12+148*e^-0.15648x)
A= 12
G = 160
k = 0.000978
nach dem Schema f(x) = (A*G)/(A + (G - A) *e^-k*g*x)
und wollte den mal in die erste Ableitung bringen
Nach dem Schema zum Ableiten von Brüchen,
f(x)=g/h --> f'(x)=g' * h - h' * g / h^2
müssten die werte sich demnach so verändern.
g = 1920
g' = 0
h = 12 + 148 * e^-0.15648x
h' = 148 * e^-0.15648
Das Ganze dann wiederum eingesetzt würde demnach so aussehen:
f'(x) = ((0 * 12 + 148 * e^^-0.15648x) - (1920 * 148 * e^0.15648)) / (12 + 148 * e^-0.15648x)^2
Vereinfacht habe ich das Ganze dann zu
f'(x) = (1920 * 148 * e^0.15648)) / (12 + 148 * e^-0.15648x)^2
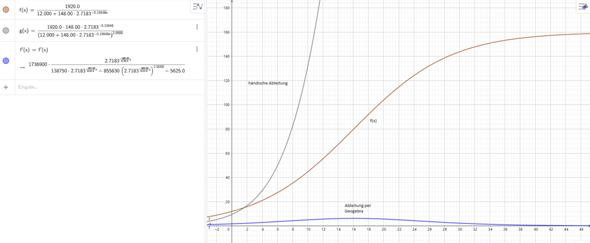
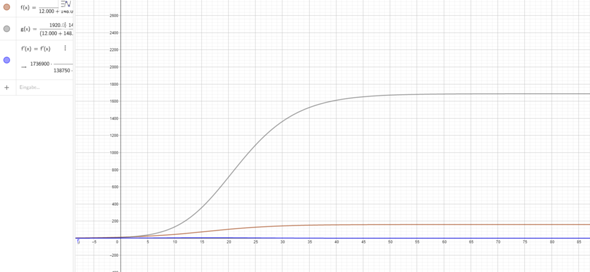
So, nun habe ich den Term in unserem Matheprogramm GeoGebra mal eingegeben, das Ganze müsste demnach die Wachstumsfunktion sein, allerdings sieht der Verlauf nicht mal Ansatzweise so aus. Ich weiß ehrlich gesagt nicht mehr weiter, und finde den Fehler dazu nicht, kann mir jemand dabei weiterhelfen oder erklären wo der Fehler liegt?
Bilder vom Graphen sind angehängt, man kann sich mit Geogebra auch die Funktion so ableiten lassen (man soll es aber auch händisch können), der Graph (blau) verläuft hier allerdings völlig anders als meine Ableitung. Eigentlich wollt ich die Aufgabe nutzen um ein Schema für den Term zu haben, da der dann ja immer gleich ist, dann wäre das damit erledigt aber es klappt leider nicht.
1 Antwort
h' ist falsch: die e-Funktion muss mit der Kettenregel abgeleitet werden. Das Ergebnis ist die unveränderte e-Potenz mal der Ableitung des Exponenten (=innere Ableitung), also bei Dir:
h'=148 * e^(-0,15648x) * (-0,15648) = ...
Die Kommazahl und die 148 würde man noch zusammen multiplizieren.
ja hab noch n Fehler gefunden g' * h wäre ja null und g* h' wird ja davon abgezogen weshalb vor das alles oben über dem bruchstrich noch ein minus musste jetzt passt alles
vielen dank fürs helfen
Stimmt, soweit habe ich nicht mehr kontrolliert, weil ja vorher schon der Fehler lag. Durch das Minus in h' wird's dann aber jetzt wieder Plus.
was genau wird ein plus? Ich habe jetzt als finalen Term (- 1920 * 148 * (-0.15648) * e ^ -0.15648 ) / (12+148 * e ^-0.15648x)^2 der optisch genau auf die erste ableitung passt die der pc errechnet hat
-1920*148*(-0,15648)=+...
In der Regel fasst man alles soweit zusammen wie möglich, d. h. diese drei Faktoren würde man wohl eher zusammenrechnen, statt ständig alles auszuschreiben, sollte man mit diesem Term weiterrechnen müssen!
ah ok danke schön, hatte eigentlich auf mathebibel.de die ableitungsregeln durch, wo drin stand dass e^x zu e^x wird
richtig, nur leider sieht man an diesen Regeln nicht, dass noch die innere Ableitung dazu kommt; so könnte man meinen, dass z. B. die Ableitung von e^(2x) auch e^(2x) sei, richtig ist aber 2e^(2x)...
das heißt dann, das h' dann mit 148 * (-0.15648 * e ^-0.15648 * x) richtig aufgeschrieben wäre