Parabel 2. Ordnung durch Wendepunkte einer Parabel der 4. Ordnung erstellen
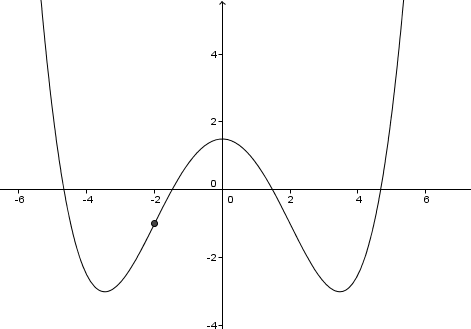
Gegeben ist eine zur y-Achse symmetrische Parabel 4. Ordnung. Von der hab ich ein Bild beigefügt. f(x)=x^4/32-(3*x^2/4)+3/2
Nun soll ich anhand der Wendepunkte (-2/-1) und (2/-1) eine Parabel 2.Ordnung erstellen. Ich dachte mir, dass der Scheitelpunlkt der Parabel auf der y-Achse liegen muss, demnach müsste die 1. Ableitung 0 sein.
Mit Geogebra kann ich dennoch die Gleichungen nicht lösen. Welchen Aspekt habe ich nicht bedacht? Bitte um Hilfe
5 Antworten
Die Frage ist doch, ob die quadratische Parabel "einfach nur" durch die Wendepunkte laufen soll oder "möglichst gut".
Die quadratische Parabel verläuft auf jeden Fall symmetrisch zur y-Achse. Daher ist der Ansatz mit p(x) = ax² + b völlig richtig. Ebenso die Bedingung p(2)=-1
Unter "möglichst gut" verstehe ich jetzt, dass die q.P. die selbe Steigung haben soll wie die vorgegebene Funktion. Dann hättest Du eine 2. Bedingung, nämlich p'(2) = f´(2) und könntest a und b eindeutig bestimmen.
Ob das so gemeint ist, weiß ich allerdings nicht. Gibt Deine genaue Aufgabenstellung da mehr her?
Ich habe raus: p(x) = -1/2x + 1
Übrigens: Deine Bedingung mit der 1. Ableitung im Scheitelpunkt würde auf die Bedingung 0=0 führen; hilft also nicht unbedingt weiter :-)
Genau, das Wort "berührt" macht den Unterschied! Damit ist der Ansatz so wie von mir vermutet.
Punkt (2|-1)? Er steht zum einen in der Aufgabe ( :-) ), zum anderen ergibt er sich aus der Symmetrie. Es kommt mathematisch auf dieselben Gleichungen hinaus, ob Du mit x = 2 oder x = -2 arbeitest (vgl. Deine Kommentare mit Ellejolka). Nur ich bevorzuge dann die positiven Werte.
f(x)=x^4/32 - 3/4 * x^2 + 3/2.
p(x):=a * x^2 +b * x + c.
- (-2/1) und (2/1) in G[p] und f'(-2) = p'(-2) und f(2)=p(2).
p'(x) = 2 * a * x + b => p'(2)= 4 * a + b und p(-2) = -4 * a + b
f'(x) = 1/8 * x^3 - 3/2 * x => f'(2) = 1- 3 = -2 und f'(-2) = -1 + 3 = 2
=> I) -2 = 4 * a + b
=> II) 2 = -4 * a + b
I + II: 2 * b = 0 <=> b = 0
II - I: 4 = -8 * a => a = -1/2.
=> p(x) = -1/2 * x^2 + 0 * x + c = -1/2 * x^2 + c
p(-2) = p(2), da symmetrisch und p(2) = -2 + c = 1, da (2/1) in G[p] <=> c = 3.
=> p(x) = -1/2 * x^2 + 3.
VG, dongodongo.
y=ax²+b → -1=4a+b ; du sollst eine Parabel finden; es gibt mehrere, die durch die Wendepunkte gehen. Vielleicht kannst du beliebiges b wählen, zB b=1
dann a=-1/2 also y= -1/2 x² + 1 wäre so eine Parabel.
Nein, ein beliebiges b darf ich bestimmt nicht wählen. Deswegen über legeich auch schon seit Stunden, was ich übersehen habe. Aber mir fällt nichts mehr ein...
Sollst Du evtl eine quadr. Parabel suchen, die durch die Wendepunkte geht, und dort die gleiche Steigung hat, wie die Parabel 4. Ordnung?
ja, f '(0) = 0 und die beiden Wendepunkte hast du auch.
die Parabel y=ax²+b
einsetzen und a und b berechnen.
Nun, das dachte ich auch. Das genau ist auch das Problem, es funktioniert nicht.
a = (-1) / 4 b - 1 / 4
b=b
Sind die Lösungen, mit denen ich absolut nichts anfange. Demnach muss es irgendwo noch eine Gleichung geben, die ich nicht entdeckt habe,
Ich habe die Wendepunkte berechnet, das ist ja keine große Sache. Das eben war die Lösung, als ich versuchte a und b auszurechnen. Doch ist das Gleichungssystem noch nicht komplett.
Ich habe: f(-2)=-1 f(2)=-1 f'(0)=0
Und aus diesen Gleichungen schaffe ich es nicht a und b auszurechnen. Bzw schafft es auch Geogebra nicht.
Ich glaub der Fehler bei mir wahr, dass ich nicht genau gelesen hab. In der Angabe steht die Parabel 'berührt' die Wendepunkte.
Allerdings ist der Wendepunkt auf W(-2/-1) also kann ich einfach f'(-2)=g'(-2) setzen? Oder wie kommst du zu dem Punkt (2/-1)?