Mathe Steckbriefaufgabe: Wendetangente durch den Ursprung bei einer achsensymmetrischen Funktion bestimmen?
Hallo! Ich habe ein ziemlich großes Verständnisproblem bei der folgenden Aufgabe: "Der Graph einer ganzrationalen Funktion 4. Grades ist symmetrisch zur y-Achse und hat in W(1|2) einen Wendepunkt, dessen Wendetangente durch den Ursprung verläuft." Also erst habe ich die allgemeine Funktionsgleichung [f(x)= ax^4+bx^3+cx^2+dx+e] aufgestellt sowie die ersten zwei Ableitungen berechnet. Anschließend habe ich b=0 und d=0 gesetzt, da die Funktion symmetrisch zur y-Achse ist (sprich achsensymmetrisch). Danach die Gleichung für den Wendepunkt aufgestellt. Das Problem ist jetzt: wie gehe ich bei der Wendetangente vor? Da diese durch den Ursprung verläuft hätte ich gedacht ich müsse die Tangentengleichung so aufstellen: g(0)=0, aber das bringt mich nicht weiter. Könnte mir jemand verraten wie ich hier vorgehen sollte? LG
3 Antworten
Mir scheinen die anderen Ansätze etwas zu kompliziert. Alternativer Vorschlag:
Der Graph geht durch W => f(1) = 2 => a + c + e = 2
Bei x = 1 ist Wendestelle => f´´(1) = 0 => 12a·1² + 2c = 0
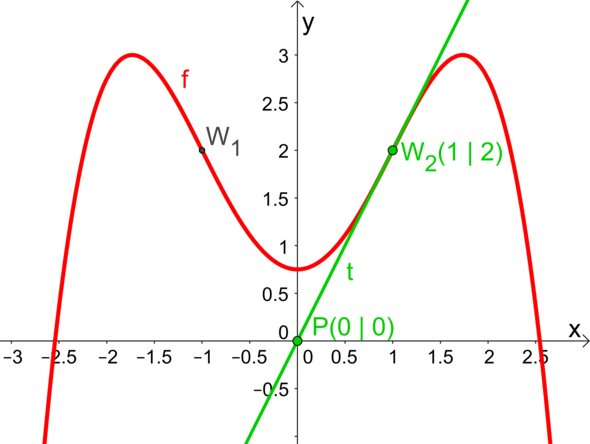
Die Wendetangente verläuft sowohl durch (1|2) als auch durch (0|0). Ihre Steigung lässt sich also berechnen (Steigungsdreieck) durch m = (2-0)/(1-0) = 2. Andererseits ist die Steigung aber auch durch die erste Ableitung an der Wendestelle gegeben. Also:
f´(1) = 2 => 4a·1³ + 2c·1 = 2
LGS lösen - fertig.
[Meine Lösung: f(x) = -1/4 x^4 + 3/2x² + 4/4.]
Die Formel für die Wendetangente ist:
t:y= f´(xo)*(x-xo)+f(x)
Mit dem Wendepunkt (1/2) (xo/f(xo)) kann man das ausrechnen.
LG
VIELLERNERIN
Wie lautet denn die urspüngliche Gleichung und deren erste Ableitung?
Warum willst du denn x wegbekommen. Du suchst doch eine Gleichung für die Wendetangente? Dann brauchst du doch das x.
Außerdem setzt du in der Formel nichts für y ein. Es ergibt sich nachher eine Funktion in der Schreibweise y=mx+c.
LG
VIELLERNERIN
Könntest Du mir vielleicht zeigen was ich wo einsetzen soll? Ich bin mir nämlich nicht sicher, ob ich es verstanden habe.
Du hast ja einmal f(x) und einmal f´(x).
Und du hast aus dem Wendepunkt (1/2): xo=1 und f(xo)=2.
Dann brauchst du noch f´(xo): also die Ableitung an der Stelle 1.
Außerdem brauchst du noch
Die Formel lautet: t(Tangente): y = f´(xo)*(x-xo)+f(x)
Du setzt folgendermaßen ein:
y = f´(2)*(x-1)+f(x)
Wenn du das ausrechnest, bekommst du die Tangente.
LG
VIELLERNERIN
Du hast schon:
- Funktion symmetrisch: f(x)= ax⁴+cx²+e
- Wendepunkt in (1; 2): f ''(1) = 12a+2c = 0 (Gleichung 1)
Dir fehlt noch:
- Wendetangente: t(x) = f '(1)·(x-1)+2 = (4a+2c)(x-1)+2
- t geht durch (0; 0): t(0)=0 ⇔ -4a-2c+2=0 (Gleichung 2)
Dann hast Du zwei Gleichungen mit zwei Unbekannten ...
Ok! Dann müsste die Gleichung wie folgt lauten:
t: 2= 4a+2c • (x-1)+2 ; aber dann bleibt ja noch das 'x', wie kriege ich das nun weg?