GRAFISCHES DIFFERENZIEREN Fkt. 3. Grades - 1. & 2. Ableitung. Wie mach ich die 2.?
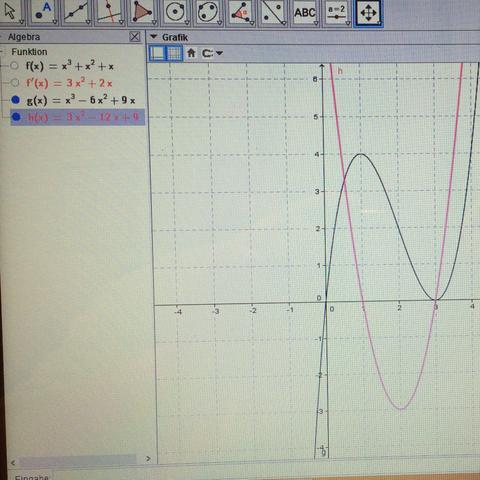
Ich bin es wieder :D, muss in meiner Prüfung grafisch differenzieren. Ist ja im Prinzip kein Hexenwerk. Jetzt hänge ich jedoch bei der 2. Ableitung.. Kann jemand anhand des Fotos mir weiter helfen? || habe für die 1. Ableitung bei HP / TP ein Schnittpunkt in der Achse, beim WP den TP.. Aber wie mach ich das bei der 2. Ableitung? (6x - 12 lautet sie, aber ich muss es ja GRAFISCH ableiten)
4 Antworten
Lieber DrAdvisor,
Wir machen in der Schule gerade grafisches Differenzieren. Also, es geht wie folgt:
- zunächst Extrema, Wendepunkte und (falls vorhanden) Sattelpunkte Markieren. Du weißt dann nämlich folgendes:
=> Extremstellen - Nullstellen der ersten Ableitung
=> Wendepunkte - Extrema der ersten Ableitung
=> Sattelpunkte - Nullstellen der ersten Ableitung
Hier hast du bei x = 1 und bei x = 3 Extremstellen und bei x = 2 einen Wendepunkt. - Weiterhin kann man an der ersten Ableitung sehen, wann die Funktion steigt und wann sie fällt. Rechnerisch ist die erste Ableitung f'(x) = 3x² -12x +9, aber das sollst du eben grafisch bestimmen. Nimm dir noch ein paar gut lesbare Punkte, lege eine Tangente durch den Punkt und bestimme in etwa ihre Steigung und trage das in das zweite KS ein wo auch schon die anderen Punkte markiert sind.
- nun kannst du schon in etwa deine Funktion zeichnen. Um nun die zweite Ableitung zu bestimmen, musst du die Steigungen der ersten Ableitungen mit einbeziehen. Es gilt außerdem:
=> Extrempunkt der ersten Ableitung - Nullstelle der zweiten Ableitung
=> Linkskrümmung bei f - Positiv bei f''
=> Rechtskrümmung bei f - Negativ bei f''
Hier hast du bei x = 2 den Extrempunkt der ersten Ableitung, also wird bei der zweiten Ableitung - eine Gerade mit der Funktionsgleichung f''(x) = 6x-12 - dort die Nullstelle sein.
Allgemein kannst du immer folgendes sagen (das könnt dir beim graphischen Differenzieren etwas nützen!):
- f'(x) < 0 => Funktion f(x) fällt
- f'(x) = 0 => Extremstelle in f(x)
- f'(x) > 0 => Funktion f(x) steigt
- f''(x) < 0 => Funktion f(x) hat eine Rechtskrümmung
- f''(x) = 0 => Funktion f(x) hat einen Sattelpunkt
- f''(x) > 0 => Funktion f(x) hat eine Linkskrümmung
- f''(xe) < 0 => Funktion f(x) hat an xe einen Hochpunkt
- f''(xe) = 0 => Funktion f(x) hat an xe einen Sattelpunkt
- f''(xe) > 0 => Funktion f(x) hat an xe einen Tiefpunkt
- etc. - der Rest fällt mit ad hoc nicht ein.
Ich hoffe ich konnte helfen - im Anhang noch ein Bild zu deiner Funktion f (blau), der ersten Ableitung f' (rot) und der zweiten Ableitung f'' (grün). Bei Fragen melde dich.
LG ShD
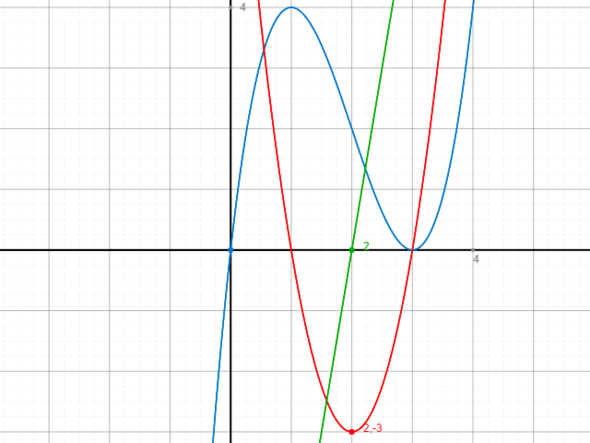
Du weißt, dass die Grundfunktion eine Funktion dritten Grades ist, dadurch ist die Ableitung eine Parabel und deren Ableitung eine Gerade. Die erste Ableitung hast du grafisch schon bestimmt. Die Parabel fällt bis zum Punkt x=2 und steigt danach. D. h. dass die zweite Ableitung, also die Gerade, die x-Achse bei x=2 schneiden muss. Vorher muss sie unter der x-Achse verlaufen, nachher über der x-Achse.
da ist irgendwas falsch; f ' muss 3x²+2x+1 heißen;
und wo f ' ein Tiefpunkt hat, hat f " eine Nullstelle
und wo f ' fällt, verläuft f " im Negativen
wo f ' steigt, da f " im Positiven.
Ah genau, jetzt weis ich immernoch nicht wie ich auf die Steigung der Geraden komme. Ich weis wie ich das rechnerisch mache.. Nur grafisch hab ich keinen Dunst
die Steigung 6 bekommst du graphisch nicht genau raus; also kann man f " graphisch nur wage bestimmen; mit Nullstelle und Verlauf von unten nach oben; siehe was ich oben geschrieben habe.
Aber ich sehe grad der Fehler ist irrelevant, da diese FKT nicht sichtbar war.. Nur die mit dem blauen Punkt..
VERDAMMT du hast Recht.. Oh Jesus wenn ich solche Fehler in der Prüfung mach krieg ich n Problem 😃 Danke jetzt hab ich auch verstanden wie man quadratisch grafisch differenziert
Hallo,
wie mostmichl schon schrieb, ist die zweite Ableitung eine Gerade, die bei x=2 eine Nullstelle besitzt (dort hat die erste Ableitung ein Minimum). Einen Punkt, um die Gerade zu bestimmen, hast Du also schon. Den zweiten könntest Du zeichnerisch dadurch erhalten, daß Du an irgendeiner Stelle des Graphen der zweiten Ableitung eine Tangente anlegst, deren Steigung Du durch ein geeignetes Steigungsdreieck durch einfaches Kästchenzählen und Dividieren ablesen kannst. Dieser Wert wäre der Funktionswert zu der Stelle, an der Du die Tangente angelegt hast. Den Punkt einzeichnen, mit dem Nullpunkt der zweiten Ableitung verbinden und fertig.
Herzliche Grüße, Willy
Danke, und woher weis ich die Steigung der Geraden? Rechnerisch weis ich wie ich drauf komme, grafisch.. Kp